Intégrales et aires
-
Mmashopha dernière édition par
Bonjour j'ai des difficultés a réaliser cet exercice, pouvez vous m'aider ?
Le plan est rapporté à un repère orthonormal (o,i,j)
Soit I(1,0). f la fonction définie sur l'intervalle [0,1] par f(x)=e^(x-1) et C sa courbe représentative dans le repère (o,i,j).
On note Δ la portion de plan comprise entre la courbe C, l'axe
des abscisses et les droites d'équation x=1 et x=0 et A, l'aire de Δ.Pour tout x∈[0,1], on note M le point de coordonnées (x,f(x))
et D(x) le domaine délimité par la droite (IM), l'axe des abscisses,
l'axe des ordonnées et la courbe C.
On désigne par g(x) l'aire de D(x).
- Calculer la valeur de A
intégrale(0;1) f(x)dx= 1-e^-1
- Calculer g(o)
Cela revient a calculer l'aire du triangle OMI lorsque M(0;f(0)), Aire OMI= 1/2e
3)Montrer, par considérations d'aire, que: g(0)≤ 1/2 A ≤g(1)
Fait- Pour tout x∈[0;1], montrer que : g(x)= 1/2(3-x)e^(x-1) - 1/e
on a
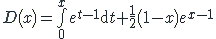
donc en calculant on trouve bien g(x)= 1/2(3-x)e^(x-1) - 1/e5a) Etudier les variations de g sur [0;1]
g'(x)= 1/2(2-x)e^(x-1)
donc g(x) est croissante sur [0;1].
b)montrer qu'il existe un unique réel α sur [0,1] tel que g(α)= 1/2A
trouver une valeur approchée de α à 0.001 près par defaut.Je n'y arrive pas.
Pouvez vous m'aider pour ces deux questions ?
Merci d'avance
-
Bonjour,
Calcule g(0) et g(1).