Analyse: fonction et trigonométrie

[Lovely_76]

Bonjour, voilà j'ai un exercice que je ne comprends pas je ne suis même pas su de savoir de quoi partir. Pour moi il s'agit d'un exercice en rapport avec la trigonométrie et les fonction.

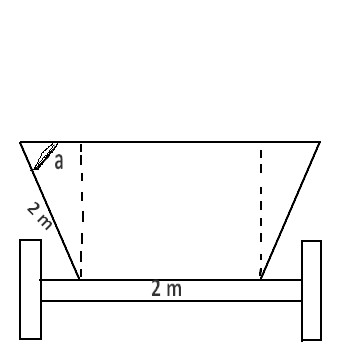
La benne d'une remorque de tracteur a une section ayant la forme d'un trapèze isocèle.
Soit f(a)l'aire de cette section, a ϵ $[0;\frac{\pi }{2}]$

1.Démontrer que f(a)= 4 sin a (cos a+1)
2.démontrer que f(a)= 8 (cos a- $\frac{1}{2}$)(cos a+1)
3.En déduire le tableau de variation de f.
4.La benne ayant une longueur de 5m, quelle est sont volume maximal en m^3

Je pense qu'il faut se servir de la formule de l'aire d'un trapèse mais je ne suis pas sur car je ne comprends pas du tout.
Aire= (B+b)*h/2
Y a-t-i quelqu'un qui peut m'aider à démarrer cette exercice. Merci

[Lovely_76]

[Noemi]

Bonsoir,

C'est bien cette formule qu'il faut utiliser.

Exprime la hauteur et la grande base en fonction de a en utilisant le trigonométrie.
Puis calcule l'aire.

[Lovely_76]

Bonjour.
Merci de cette aide. J'ai eu un peu de mal mais je pense avoir qulque chose. Déja j'ai placé des poin sur la figure pour pour voir exprimer la bae et la hauteur plus facilement.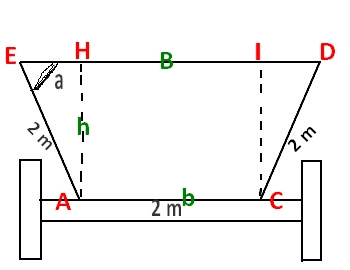

Donc pour exprimer la hauteur:
$sina=\frac{oppose}{hypotenuse}=\frac{ah}{ae}$
$ah=sina<em>ae=sina</em>2$
Après pour exprimer la base en fonction de a il faut d'abord exprimer EH en fonction de a car B= b+EH+ID et ID=EH
Donc $cosa=\frac{adjacent}{hyptenuse}=\frac{eh}{ae}$
$eh=cosa<em>ae=cosa</em>2$
D'où $b=b+2<em>eh=2+2(cosa</em>2)$

Ensuite pour l'aire:
A= (B+b)h/2
$a=\frac{((2(cosa</em>2)+2)+2)<em>sina</em>2}{2}$
Est-ce bien comme cela?

[Noemi]

C'est correct;

Simplifie le résultat.

[Lovely_76]

$\frac{(2(cosa<em>2)+2+2)</em>(sina<em>2)}{2}=\frac{((2</em>2cos+4)<em>2sina)}{2}=\frac{4cos+4</em>2sina}{2}$
Je ne sais pas si ma simplication est correct car j'ai un eu de mal avec les calculs de cosinus et sinus. Est-ce qu'une fois simplifier je trouve le résultat de la quiestion n°1?

[Noemi]

2 sina /2 = sina

simplifie l'expression entre parenthèses

[Lovely_76]

Je ne comprends pas trop.
$\frac{((2(cosa<em>2)+2)+2)</em>(sina<em>2)}{2}=\frac{(2cosa</em>2+2)+2)\ast 2sina)}{2}=\frac{(4cosa+4)<em>2sina}{2}=\frac{8cosa</em>sina+8}{2}$
Je n'arrive pas à trouver $4sina(cosa+1)$
J'ai beau chrcher je 'arrive pas à aboutir cette simplification.

[Lovely_76]

Je pese avoir une autre petite idée:
$\frac{8cosa<em>sina+8}{2}=\frac{8coa</em>sina}{2}+\frac{8}{2}=4cosa\ast sina+4=4sina(cosa+1)$
Mais je sais pas si j'ai le droit de passé de l'avant drniere etape de calcul à la derniere?

[Lovely_76]

Je me rencontre que dans mes calcules precedants ils y a des erreurs c'est pourquoi je ne trouver pas le bon résultat.
Donc:
$f(\alpha )=\frac{(4cs\alpha +2+2)<em>2sin\alpha }{2}=\frac{8cos\alpha sin\alpha +4sin\alpha +4sin\alpha }{2}=\frac{8cos\alpha </em>sin\alpha +8sin\alpha }{2}$
$f(\alpha )=\frac{8cos\alpha \ast sin\alpha }{2}+\frac{8sin\alpha }{2}=4cos\alpha \ast sin\alpha +4sin\alpha =4sin\alpha (cos\alpha +1)$

[kate-02]

Comment fais-tu la deuxieme question?

[Noemi]

C'est correct.

[Lovely_76]

Euh merci. Parcontre pour la 2° il faut calculer la dériver? JJ'ai essayer mais sa donne rien qui puisse ressembler à celle de lénoncé

[mtschoon]

Bonjour,

Je pense qu'à la 2) , tu as voulu écrire f ' (a)=...

Pour la dérivée de f :

4 est une constante.

Pour calculer le dérivée , utilise la dérivée d'un produit

U(a)=sina donc U'(a)=cosa

V(a)=cosa+1 donc V'(a)=-sina

Tu calcules et tu remplaces sin²a par 1-cos²a

Tu dois trouver :

$f^{\prime }(a)=4(2co{s}^{2}a+cosa-1)$

En factorisant , tu obtiens l'expression de l'énoncé

[Lovely_76]

Bonsoir,
Effectivement, ils'agit de f'(a).
Ensuite donc f(a)= 4sina(cosa+1)
Donc si j'ai bien compris:
$f^{\prime }(a)=4\ast [(cosa<em>cosa+1)+(sina</em>(-sina)]=4\ast [(co{s}^{2}a+1)+(-si{n}^{2}a)]=4\ast [(co{s}^{2}a+1)+(-(1-cos2a))]=4\ast (co{s}^{2}a+1-1+cos2a)$
Mais je n'arrive pas à aboutir a quelque chose comme vous. En plu normalement sin²a est égal à (1-cos2a)/2, non?

[mtschoon]

Il faut voir le but recherché.

Si tu transformes avec des cos2a , tu ne trouveras pas ce qu'on te demande...

Il faut que tu n'aies que des "cosa"

Rappel :

$si{n}^{2}a+co{s}^{2}a=1doncsi{n}^{2}a=1-co{s}^{2}a$

[kate-02]

Moi j'ai réussi a trouver f'(a)=4(2cos²a+cosa-1)
Quand tu developpe ta dérivée avec la formul u'v+uv' tu as :
[cosa*(cosa+1)...
Tu dois faire cosacosa+cosa1. Se qui te donne cos²a+cosa et pas cos²a+1

[Lovely_76]

En effet donc
$f^{\prime }(a)=4\ast [(cosa\ast (cosa+1))+(sina\ast (-sina))]=4[co{s}^{2}a+cosa+(-si{n}^{2}a)]=4[co{s}^{2}a+cosa+(-(1-co{s}^{2}a))]=$
$f^{\prime }(a)=4[co{s}^{2}a+cosa+(-1+co{s}^{2}a)]=4(co{s}^{2}a+cosa-1co{s}^{2}a)=4(2co{s}^{2}a+cosa-1)=8co{s}^{2}a+4cosa-4=8(cosa-\frac{1}{2})(cosa+1)$

Est-ce correct?

[Lovely_76]

Oui je sais j'avait trouvée!

[kate-02]

Oui je vois ^^