Résoudre un problème avec les suites en utilisant la méthode de Héron
-
Tterminales dernière édition par Hind
Bonsoir à tous, voilà j'ai un exercice à faire mais je n'y arrive pas donc j'ai besoin de votre aide
 le voici:
le voici:"soit un rectangle dont l'aire est égale à 2. si sa largeur est l, sa longueur est 2/l. La moyenne des 2 dimensions est donc 1/2*(l+(2/l)).
on construit alors un nouveau rectangle d'aire 2 dont la largeur est égale à cette moyenne. on calcule la longueur de ce rectangle, puis la moyenne des 2 dimensions, etc...En itérant le procédé, les rectangles ainsi construits se rapprochent d'un carré d'aire 2, donc de côté racine carré de 2. 2\sqrt{2}2.
En terme modernes, cet alogorithme de calcul approché de racine carré de 2. 2\sqrt{2}2 utilise la suite u définie sur N par:
Un+1=1/2*(Un+(2/Un)) et U0=l
où l est un réel strictement positif-
a l'aide de la courbe representative de la focntion x →1/2*(x+(2/x)). vérifier graphiquement que la suite u semble converger. vers quoi?
-
montrer pour tout entier n≥1 , Un≥ à racince carré de 2 (√2).
3°) montrer que la suite u est décroissante; conclure quant à la convergence de la suite u. on determinera sa limite.
4) a) montrer que pour tout entier n:
Un+1-√2 ≤ (1/(2√2))(Un- √2)² ≤ 1/2 (Un- √2)²b) montrer par récurrence que pour tout entier n≥1 :
Un -√2 ≤ (1/2)2n^{2n}2n * (Un- √2)c) on choisit ici l=2. au bout de combien d'itérations sera t-on que Un est une valeur approchée de √2 à 10−910^{-9}10−9 prés?
5° ALGO
a)pour tout précision e>0, on souhaite connaitre le nombre d'interactions pour lequel on est sûr que Un est une valeur approchée de √2 à e prés. on propose l'algorithme ci contrevariables: n: entier:e,l:réels
début
entrer (l;e);
n←0n\leftarrow 0n←0
tant que
(12)2n\left(\frac{1}{2} \right)^{2n}(21)2n × ≥(l−2)(l-\sqrt{2})(l−2)≥ e
faire n←n+1n\leftarrow n+1n←n+1FinTantQue
afficher (n);
finjustifier qu'il permet de résoudre le probléme.
b) programmer l'algorithme, puis l'éxecuter pour:
i)l=101 et e=10−410^{-4}10−4
ii) l=50 et e=10−410^{-4}10−4
c) commenter les résultats obtenusvoilà après avoir écrire ce gros pavé, j'espere que quelqu'un va m'aider

j'ai commencé à tracer les triangles pour mieux comprendre le probléme et la courbe de la focntion x →1/2*(x+(2/x))
apres j'ai besoin de votre aide pour la convergence de cette courbe et le reste de l'exercice
merci à tous de votre aide!

-
-
Bonsoir terminales,
Pour la convergence, c'est une étude graphique.
-
Tterminales dernière édition par
C'est pour la suite que je n'arrive pas. Merci noemi de m'avoir répondu

-
Pour la question 2, tu supposes que la suite tend vers l et tu calcules l.
-
Tterminales dernière édition par
Comment je fais pour calculer l? En le remplaçant par un nombre?
-
non, tu résous
l = 1/2(l + 2/l)
-
Tterminales dernière édition par
Ok J'arrive
-
Tterminales dernière édition par
J'arrive pas trouvé une valeur de l
 pourtant c'est simple
pourtant c'est simple
-
2l = l + 2/l,
réduis au même dénominateur puis résous l'équation du second degré.
-
Tterminales dernière édition par
l=l/2 + 4/l c'est ça?
-
Tterminales dernière édition par
c'est pas ça?
-
Tterminales dernière édition par
je sais plus svp

-
2x = x + 2/x donne
x = 2/x
soit x² = 2
donc comme x > 0, x = ....
-
Tterminales dernière édition par
x=√2
c'est ça?
-
Oui
-
Tterminales dernière édition par
je fais comment pour la 3)?

-
Etudie les variations de la fonction f
-
Tterminales dernière édition par
gaphiquement ou en calculant?
-
Par le calcul, dérivée, sens de variation.
-
Tterminales dernière édition par
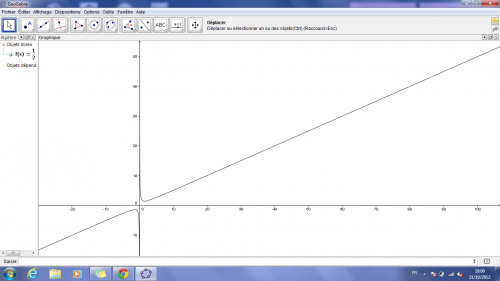
j'ai ça mais je ne sais pas comment trouver les variations de f
-
Tterminales dernière édition par
la dérivée de 1/2 est 0
comment je fais déja pour trouver lé dérivée de x+(2/x)? :-$
:-$
-
Calcule la dérivée de x puis de 2/x
-
Tterminales dernière édition par
x=1
2/x= 2 (x ^ (-1))
apres je fais comment?
-
Tterminales dernière édition par
je pense que je dois faire un tableau non? mais je ne sais pas trop comment le faire
-
la dérivée de x est 1, la dérivée de 2/x est -2/x²
donc la dérivée de la fonction est ....
-
Tterminales dernière édition par
-2/x²
-
Tterminales dernière édition par
please noemi aide moi c'est pas ça?
-
non la dérivée est 1/2 (1-2/x²)
-
Tterminales dernière édition par
ah oui je vois
comment je fais apres poiur montrer que la suite u est decroissante
-
Etudie le signe de la dérivée et le sens de variation.
-
Tterminales dernière édition par
je fais comment ?

-
Résous f'(x) = 0 et étudie le signe de la dérivée sur chaque intervalle de définition.
-
Tterminales dernière édition par
Je pense que je dois faire un tableau non? mais je ne sais pas trop comment le faire
-
Fais un tableau de variation avec la valeur interdite et les valeurs qui annulent la dérivée.
-
Tterminales dernière édition par
quelle est la valeur interdite? c'est 1? je dis ça car 1 est la dénominateur de 2/x
-
Non 0.
-
Tterminales dernière édition par
j'arrive pas à faire mon tableau

-
Tterminales dernière édition par
voilà ce que j'ai fais mais j'arrive pas
-
Pour le sens de variation de la suite compare un+1/un avec 1
-
Tterminales dernière édition par
je comprends pas quand tu dis Un+1/un AVEC 1