etude de fonction (fonction valeur absolue- fonction polynome de degré 2)
-
Hhelloladies dernière édition par
Bonjour à tous. J'ai l'exercice suivant à faire. Je vous ai mis mes réponses:
-
Etudier les variations de la fonction u définie sur mathbbRmathbb{R}mathbbR par u(x)=2x²+2x-4
ma réponse: la forme canonique de u(x) est 2(x+1/2)²-9/2
le coefficient de x² est positif donc u admet un minimum qui est -9/2. Il est atteint pour x=-1/2
de -∞ à -1/2 :décroissante
de -1/2 à +∞ :croissante -
Etudier le signe de u(x) suivant les valeurs de x.
ma réponse: le discrimant de 2x²+2x-4 est positif (Δ=36) donc le polynome admet 2 racines qui sont -2 et 1.
u(x)>0 si x<-2 ou si x>1
u(x)<0 si -2<x<1
u(x)=0 si x=-2 ou si x=1 -
En déduire les variations de la fonction z défine pour tout réel x par z(x)=l2x²+2x-4l
ma réponse: si x<-2 ou si x>1 z(x)=u(x)
si -2<x<1 z(x)=-u(x)=-2x²-2x+4 sur l'intervalle -2;1 z(x) admt un maximum en (-1/2;9/2)
de -∞ à -2: décroissante
de -2 à -1/2: croissante
de -1/2 à 1: décroissante
de 1 à + ∞: croissante -
Tracer la représentation graphique de la fonction u puis celle de z
u(x): minimum (-1/2;-9/2) x1=-2 x2=1 courbe en forme de u tournée vers le haut
z(x) : maximum (-1/2;9/2) x1=-2 x2=1 courbe en forme de u tournée vers le bas
J'aimerai avoir votre vis sur mes réponses et des conseils. Merci d'avance.

-
-
Bonjour helloladies,
Les réponses sont correctes sauf pour la représentation de z pour x < - 2 et x >1 qui correspond à cette de u.
-
Hhelloladies dernière édition par
Peux tu m'expliquer comment faire les représentations graphiques s'il te plaît?
-
Pour la fonction u, c'est une parabole.
Pour la fonction z, seule la partie comprise entre -2 et 1 change, tu traces le symétrique par rapport à l'axe des x. .Les deux graphes ont une partie commune, celle pour x < _2 et pour x > 1.
-
Hhelloladies dernière édition par
donc pour la fonction z je trace une parabole qui s'arrête à -2 et 1
-
Hhelloladies dernière édition par
et qui est tournée vers la bas
-
Non,
La partie x < -2 et x > 1 est commune au deux graphes. Seule la partie comprise entre -2 et 1 est à inverser.
-
Hhelloladies dernière édition par
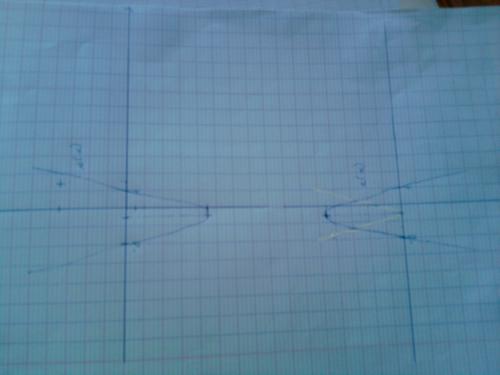
-
Pas très compréhensible le dessin.
Pour z, le graphe est au dessus de l'axe des x.
-
Hhelloladies dernière édition par
dsl pour la qualité de la photo
-
Hhelloladies dernière édition par
Bonjour, je voudrais savoir pourquoi pour la fonction z la courbe est elle seulement au dessus de laxe des abscisses? Pourquoi n'est elle pas en dessous aussi?
-
la fonction z est une valeur absolue et une valeur absolue est toujours ≥ 0 !
-
Hhelloladies dernière édition par
c'est à dire? Je n'ai pas compris. Dsl pour les questions mais je souhaite vraiment comprendre ce devoir.
-
A quoi est égal lxl ?
si x ≥ 0 ;....
si x < 0 ; .....
-
Hhelloladies dernière édition par
si x>0
lxl=x
si x<0
lxl=-x