Montrer que des droites sont non coplanaires
-
Ssophia33 dernière édition par Hind
Bonjour j'ai besoin d'aide pour un exercice :
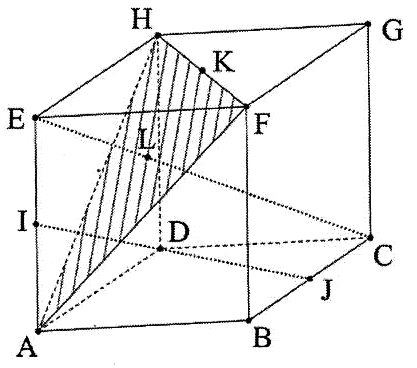
Voici la figure :Description de la figure dans l'espace muni du repère orthonormé :
(A;AB;AD;AE)
ABCDEFGH désigne un cube de côté 1.
On appelle le plan (AFH).
Le point I est le milieu du segment [AE],
Le point J est le milieu du segment [BC],
Le point K est le milieu du segment [HF],
Le point O est le milieu de [AB]
Le point L est le point d'intersection de la droite (EC) et du plan .On me demande de montrer que (IJ) et (EC) sont non coplanaires
J'ai trouvé mais l'autre question je n'y arrive pas du tout :Soit M le point tel que : 3EM(vecteur) = 2EO (vecteur)
Montrer que 3IL = EI + AB (vecteurs)Merci de votre aide
-
Bonjour sophia33,
Ou est placé le point O ?
Indique tes calculs.
-
Ssophia33 dernière édition par
Le point O est le milieu de [AB] il était à rajouter, il manquait sur la figure.
I(0;0;1/2)
J(1;1/2;0)
E(0;0;1)
C(1;1;0)Soit IJ ( 1;1/2;-1/2) un vecteur directeur de (IJ) et EC(1;1;-1) un vecteur directeur de (EC)
IJ et EC non colinéaires donc (IJ) et (EC) sont sécantes ou non coplanaires.
représentation paramétrique de (IJ)
x=t
y=1/2t
z=1/2-1/2treprésentation paramétrique de (EC)
x=k
y=k
z=1-kM(x;y;z) ∈ (IJ)∩(EC)⇔ t=k
1/2t=k
1/2-1/2t =1-kLe système n'a pas de solution donc (IJ) et (EC) sont non coplanaires.
Je ne sais pas comment procéder pour montrer que 3IL=EI+AB
-
Vérifie l'énoncé :
la relation : 3IL=EI+AB ?
-
Ssophia33 dernière édition par
Oui excusez-moi
Soit M le point tel que : 3EM=2EO
Montrer que 3IM=EI+ABJe pense que pour trouver les coordonnées de M je dois faire :
3EM( xM-0) = 2(1/2) car O(1/2;0;0)
(yM-0) (0)
( zM-1) (-1)ce qui donnerait 3xM=1
3yM=0
3(zM-1)=-2donc xM=1/3
yM=0
zM=1/3M(1/3;0;1/3)
Je dois procéder comme celà ?
-
oui, tu peux procéder avec les coordonnées des points.