trigonométrie-angles orientés

Bonjour, j'ai un problème avec une exercice :

ABC est un triangle rectangle en A de sens direct tel que (BA;BC) = -π/6 et le triangle ACD est équilatéral de sens direct , en voici la figure ci-dessous :

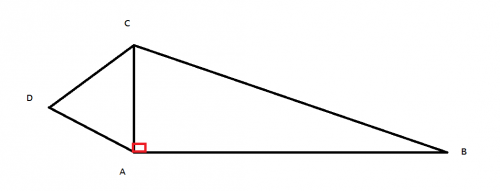
$fichier math$

Je dois donner en justifiant le calcul la mesure principale des angles orientés :

(AD;AB)
(DC;AC)
(DC;BA)
(CA;CB)

pouvez-vous m'aider ?

Bonjour,
(AD,AB) = 360 -90-60= ....

(AD;AB) = 360 - 90 - 60 = 210 ° = 7π/6 ?

(Comment avez-vous fait pour trouver 90 ° et 60 ° ? Je ne sais pas où positionner mon rapporteur ...)

Bonjour,

Comme je passe par là, en attendant que Noemi soit de retour ici pour te répondre, je regarde la question.

Je suggère d'utiliser les radians au lieu des degrés vu que l'énoncé parle de -π/6 (il s'agit donc de radians)

Pour la 1 : utilisation de la relation de Chasles relative aux vecteurs

$\text{(\vec{ad},\vec{ab})=(\vec{ad},\vec{ac})+(\vec{ac},\vec{ab}) [2\pi]$

Chaque angle géométrique du triangle ADB vaut 60° c'est à dire π/3 radians ; tu en déduis la valeur de l'angle orienté utilisé
Le triangle ACB est rectangle en A ; tu en déduis la valeur de l'angle orienté utilisé

$\text{(\vec{ad},\vec{ab})=-\frac{\pi}{3}-\frac{\pi}{2}=... [2\pi]$

Tu déduis la valeur de la détermination principale de l'angle (comprise entre -∏ et ∏)

Essaie de poursuivre.

Je vous remercies d'avoir prit le temps de me répondre avec des explications !

Si je ne me trompes pas, alors la suite devrait être :

(AD,AB) = -π/3 - π/2 = 5π/6 [2π]
(DC;AC) = (CD;CA) = π/3 [2π]
(DC;BA) = ?
(CA;CB) = π/3 [2π]

est-ce bien cela ?
merci

Pour la première réponse, revois le signe final

Oui pour le deuxième réponse et la quatrième réponse

Pour la troisième, tu décomposes à ta guise.

Par exemple, en utilisant le résultat (-5∏/6) de la première question :

$\text{(\vec{dc},\vec{ba})=(\vec{dc},\vec{da})+(\vec{da},\vec{ba}) [2\pi]=...$

N'oublie pas d'indiquer, dans chaque question, la mesure principale.

J'ai oublié le signe négatif à la première question.

Oui, pour le troisième j'y ai songé, cela fera alors :

(DC,BA) = -π/3 - ... Je ne trouves pas la propriété correspondante à (DA,BA) sur ma leçon !

Tu peux utiliser :
(DC;BA) = (DC;CB)+ (CB;BA)

La proposition de Noemi va très bien aussi ! tu fais à ta guise.

Pour $(da⃗,ba⃗)(\vec{da},\vec{ba})$ , comme je te l'ai indiqué, tu utilises la réponse à ta première question

$\text{(\vec{da},\vec{ba})=(\vec{ad},\vec{ab})=-\frac{5\pi}{6} [2\pi]$

(DC;BA) = (DC;DA) + (DA;BA) = (DC;DA) + (AD;AB) = -π/3 + -5π/6 = π/2 [2π]

?

Tu as fait une erreur dans les signes qui fausse ta réponse.

-π/3 + (-5π/6)=-∏/3-5∏/6=-2∏/6-5∏/6=.......

7π/6 !

Oui .

$\text{(\vec{dc},\vec{ba})=-\frac{7\pi}{6} [2\pi]$

Cela veut dire :

$\text{(\vec{dc},\vec{ba})=-\frac{7\pi}{6}+2k\pi , k\in z$

Comme je te l'ai indiqué, vu que l'énoncé te demande les mesures principales, pour chaque angle, il faut que tu indiques la mesure comprise entre -∏ et +∏

Tu peux nous donner les quatre mesures principales que tu as trouvées , si tu veux une vérification.

Ce ne sont pas celles que nous venons de trouver ?

Un angle orienté de vecteurs a une infinité de mesures.

Comme je te l'ai déjà dit, la mesure principale est la mesure comprise entre -∏ et +∏.

Pour la 1, la 2 et la 4 les mesures écrites -5∏/6, ∏/3 et ∏/3 sont donc les mesures principales.

Pour la 3, la mesure -7∏/6 écrite n'est pas la mesure principale (car non comprise entre -∏ et +∏) .

$\text{(\vec{dc},\vec{ba})=-\frac{7\pi}{6}+2k\pi, avec k \in z$

Trouve la valeur qu'il faut donner à k pour que la mesure soit comprise entre -∏ et +∏ (c'est simple) . Tu peux bien sur t'aider d'un schéma .

C'est quelque chose que j'ai normalement déjà apprise en classe, si je me souviens bien, en utilisant la méthode de mon professeur :

-1 > -7/6 > -2

-1π > -7/6π > -2π

je choisis le chiffre paire : (donc j'ajoute 2π)

π > -7/6π + 2π > 0

Donc la mesure principale de -7/6π est 5π/6 ou encore pour respecter votre notation :

(DC,BA) = -7/6π + 2*1π, avec k ∈ Z.

Est-ce bien cela ?

Avec la méthode que je t'indique, c'est pour k=1 que tu obtiens la mesure principale.

Et c'est bien 5∏/6 cette mesure.

Merci beaucoup !

De rien !