Calculer l’aire exacte du domaine colorié à l'aide des intégrales

[firstchil974]

Bonsoir à tous,
J'ai un exercice à faire pour la rentrée de niveau terminale S. J'ai déjà réalisé quelques démarches mais je n'arrive pas à conclure.

Voici l'exercice:
Calculer l’aire exacte du domaine colorié
ci-contre, sachant que :
● Cf est la représentation graphique d’une
fonction polynomiale de degré deux ;
● Cf passe par les points C, D et E,
de coordonnées entières ;
● la droite d passe par les points A et B,
de coordonnées entières.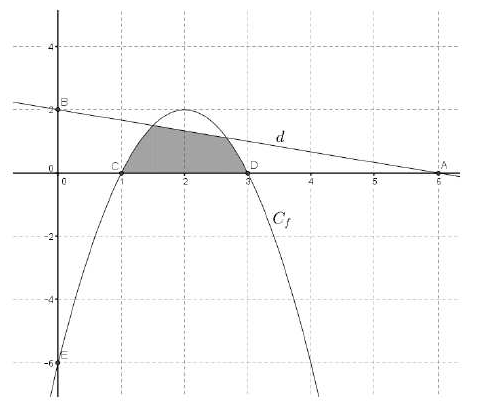

A l'aide de l'énoncé et de la figure j'ai pu réalisé la démarche suivante:
On a les points: A(6;0) B(0;2) C(1;0) D(3;0) et E(0;-6)
Avec ces points, j'ai commencé par déterminer les équations de la droite d et de la courbe représentative.
Pour la droite d, j'ai trouvé l'équation: y=-(1/3)x + 2
Pour Cf, j'ai trouvé l'équation: y= -2x² + 8x - 6

Ensuite, j'ai cherché les deux points d'intersections entre ces deux courbes à l'aide de l'équation:
-(1/3)x + 2 = -2x² + 8x -6
dont les solutions sont x(1)=3/2 et x(2)=8/3

Après cela, j'ai déterminé l'aire totale du domaine délimité par Cf, l'axe des abscisses et les droites d'équations x=1 et x=3 par une intégrale et j'ai trouvé 8/3.
( Pour primitive de f, j'ai F(x)= -(2x³/3) + 4x² -6x ).

Mais c'est ici que je bloque, je n'arrive pas à déterminé l'aire exacte du domaine colorié sur la figure. Je pense qu'il faudrait soustraire à l'aire totale que j'ai trouvé avec l'aire du domaine délimité par Cf, la droite d et les droites d'équations x=3/2 et x=8/3. Mais je ne sais pas du tout comment calculer cette dernière.

Je vous remercie d'avance pour votre aide.

[mtschoon]

Bonjour,

Effectivement, ta méthode bloque.

Je te conseille de décomposée l'aire demandée en 3 parties dont les aires sont calculables

$\bigint_1^{\frac{3}{2}}f(x)dx+\bigint {\frac{3}{2}}^{\frac{8}{3}}(-\frac{1}{3}x+2)dx+\bigint{\frac{8}{3}}^{3}f(x)dx$

Bons calculs.

[firstchil974]

Bonjour mtschoon,

Je n'avais pas pensé à cette démarche. Merci beaucoup de votre aide !

[mtschoon]

De rien !

Bons calculs (et bonne rentrée)