Les équations des tangentes

Soient (C) un cercle de centre O (1,3) et de rayon R=2 et A (0,6) un point dans le plan (P) rapporté à un repère orthonormé (O,I,J)
Donc je dois trouver les équations des droits (T1) et (T2) tangentes de (C) passants par A.

Bonjour Ghizlane,

Quelle relation y a t'il entre les vecteurs directeurs (ou coefficients directeurs) de deux droites perpendiculaires ?

Salut @noemi

On connaît l'équation de la droite (d1) : Y = a1x+b1

On sait que le produit des coefficients directeurs de deux droites perpendiculaires est égal à : - 1

Le coefficient directeur de (d1) est a1, et celui de (d2) est a2.

Donc : si a1 x a2 = - 1 alors les droites (d1) et (d2) sont perpendiculaires

Ghizlane ,

Utilise cette relation en prenant le point M(x;y) pour point d'intersection de la tangent et du cercle.
N'hésite pas à proposer tes questions ou éléments de réponse si tu souhaites des explications ou une vérification.

Bonjour,

Seulement une réflexion qui n'a rien à voir avec les calculs commencés pour trouver les équations des deux tangentes.
Je ne veux pas interférer dans les calculs, sinon l'explication devient confuse et perd en efficacité

Les données n'ont pas été choisies pour que les équations de ces tangentes soient très belles...
Je finis même par me demander si ce sont vraiment les équations qui sont demandées...

La construction des deux tangentes (sans passer par les équations), elle, est très simple.
Je la signale.

Schéma :
Cercle (en rouge) de centre O et de rayon 2
B milieu de [OA].
Pour la construction : Cercle (en pointillés) de diamètre [OA],
C et D points d'intersection des deux cercles .
Vu que $\bot (CO)$ et $\bot (DO)$ , les tangentes cherchées sont (AC) et (AD)

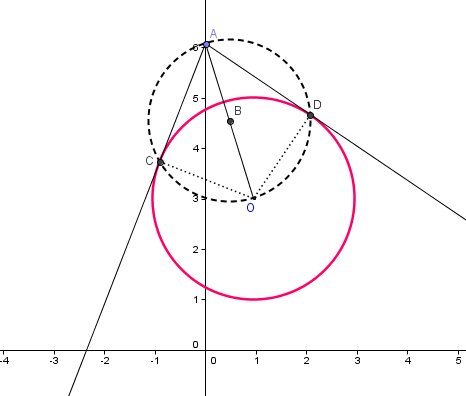
Bonne aide, Noemi, si la suite des calculs est demandée.