Application de la dérivation

Soit f la fonction définie sur $+\infty[$ par f: x -> $12x2+4\frac{12}{x^2+4}$

On note sa courbe représentative. Soit M appartient à Cf et H son projeté orthogonal sur l'axe des abscisses. Le but est de déterminer l'aire maximale de OMH, ainsi que la ou les positions du point M rendant cette aire maximale.

On choisit $x_M$ comme variable et on pose $x = x_M$ .

Déterminer une expression de la fonction A=aire( OMH).
préciser l'ensemble de définition de A.
Déterminer les variations de A sur son ensemble de définition.
Répondre au problème posé.

Voilà, sachant que le graphique dont il est question montre un triangle rectangle qui en abscisse part de l'origine à 1.5 (la base) et que la hauteur HM va de 1.5 en abscisse et monte jusqu'à 2 en ordonné.
Je sais comment calculer l'aire d'un triangle rectangle mais j'ai beaucoup de difficultés avec cet exercice, si quelqu'un pourrait m'aider je l'en remercie d'avance.

Bonsoir Akk,

Exprime MH et OH en fonction de x puis détermine l'expression de A.

Bonjour Noemi,
Comme j'ai un peu de temps, je viens de mettre des codes LaTex dans l'énoncé et joins un schéma.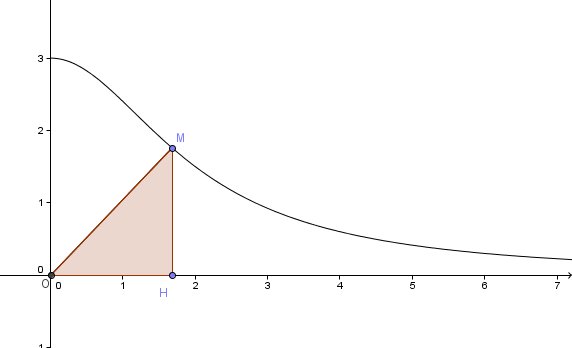

Bon travail avec Akk

Merci de votre aide, j'ai bien exprimé l'aire de ce triangle rectangle avec x mais je bloque sur le domaine de définition de cette fonction.

Bonjour akk,

Indique tes résultats.
Analyse s'il existe des valeurs qui n'ont pas d'images.

Ce qu'il me manque surtout c'est de savoir comment trouver l'aire maximale et les positions de M qui font que celle-ci est maximale, j'aimerais que quelqu'un m'aide sur cela si possible

je pense avoir trouvé que pour la question 1) il s'agit de 6x/(x²+4) et pour le 2) que le domaine de def était de ]0; + infinie[
pour le 3) j'ai donc calculer la dérivé de la formule et est trouvé -6x²+24/(x²+4)²
ensuite, j'ai trouvé les racines en faisant = 0 et ai trouver x1= 2 et x2= -2 et ensuite je bloque à la 4) donc

Akk

Pour la question 3), il est demandé les variations de la fonction.
Etudie le signe de la dérivée et construis le tableau de variation.

L'analyse du tableau de variation permet de répondre à la question 4).