Exo maths Géométrie plane

Bonsoir,
J'ai un exercice en maths que je n'est pas compris le voici

On considère un triangle non aplati ABC et M0 un point du côté [AB]. On effectué la construction suivante:
(M0 M1) est parallèle à (BC),
(M1 M2) est parallèle à (AB),
(M2 M3) est parallèle à (AC),
(M3 M4) est parallèle à (BC), etc.
Par ce procédé, fini-on par <<retomber>> sur le point initiale M0 ?
Voila je suis bloqué je ne sais pas comment faire. Me donner une piste m'aider s'il vous plaît merci.

Bonsoir, massymb

As tu fait une figure ?

@Noemi bonsoir oui il ya une figure juste à côté de l'exercice mais je sais pas comment la poster ici

Essai de faire une figure.

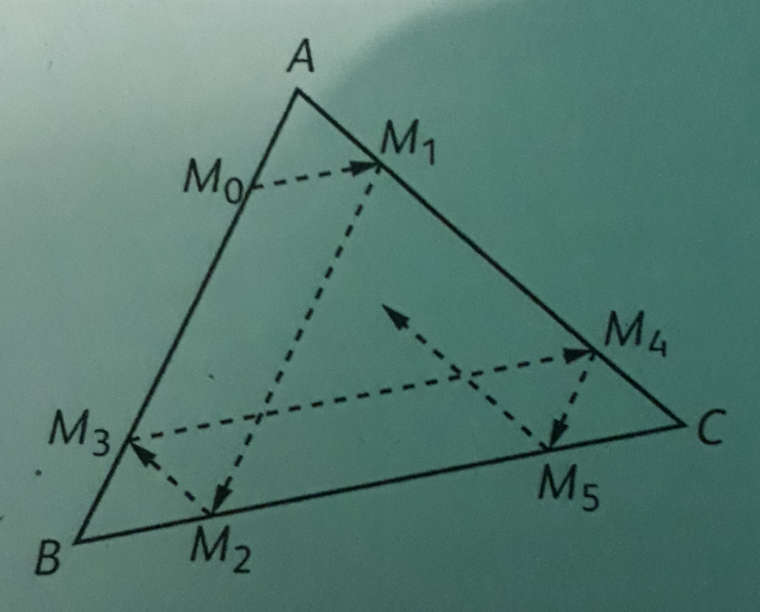
Voila la figure donnée

Quand je fait une figure je retombe sur MO le point de départ

Je n ais pas compris comment procéder pour repondre à la question

As tu pris un triangle quelconque ?

Oui triangle quelconque

Parceque je ne vois pas comment utiliser des calculs ou comment résonner

Tu le démontres en utilisant la propriété de Thalés.

D'accord voila ce que j'ai fait c'est un début
y= AM1
AM1-> AMO/y=AB/AC
AM1 = (AC × AMO)/AB

Tu poursuis jusqu'a $M_6$ , il faut démontrer que $AM_6 = AM_0$
donc que le point $M_6$ est confondu avec le point $M_0$ .

D'accord je vais essayer

Bonsoir alors voila je suis bloqué je ne sais pas comment continuer

@Noemi Je poursuis mais je m'emballe dans des choses et me perd j'ai besoin d'aide s'il vous plaît. merci d'avance.

Pour chaque construction, tu écris les rapports correspondants :
$AM0AB\dfrac{AM_0}{AB}$ = $AM1AC\dfrac{AM_1}{AC}$

$AM1AC\dfrac{AM_1}{AC}$ = $BM2BC\dfrac{BM_2}{BC}$

$BM2BC\dfrac{BM_2}{BC}$ = $BM3AB\dfrac{BM_3}{AB}$

$BM3BA\dfrac{BM_3}{BA}$ = $CM4AC\dfrac{CM_4}{AC}$

......

$CM5CB\dfrac{CM_5}{CB}$ = $AM6AB\dfrac{AM_6}{AB}$

comme tous les rapports sont égaux, tu en déduis la conclusion

$AM0AB\dfrac{AM_0}{AB}$ = $AM6AB\dfrac{AM_6}{AB}$

donc .....

D'accord ducoups en conclusion je met:
-par ce procédé tous les raport son égaux donc le point M6 et et le même que le point M0 donc confondu.

@massymb,

Tu déduis $AM_0$ = $AM_6$ , donc les points $M_0$ et $M_6$ sont confondus
donc on retombe sur le point initial.

@Noemi D'accord merci beaucoup de votre aide !