fonction avec logarithme népérien, dépendant d'un paramètre
-
MMamadou Saliou dernière édition par mtschoon
Bonsoir ,
J'ai un exercice que j'ai pas compris
On me demande de montrer que les courbes (Cn) passent par trois points fixe. Ona:
Fn(x)=n(lnx)^n
Merci!Remarque de la modération : Vu l'erreur d'énoncé faite par Mamadou Saliou avant sa modification, les premières réponses sont données avec Fn(x)=(lnx)nF_n(x)=(lnx)^nFn(x)=(lnx)n
-
Bonjour Mamadou-Saliou,
Si l'image non transmisse correspond à la représentation graphique de quelques fonctions, tu dois remarquer trois points particuliers :
A(1; 0) B (e ; 1) et C(1/e ; -1)
Il te reste à faire la démonstration.
-
mtschoon dernière édition par mtschoon

Bonjour Mamadou Saliou et bonjour Noemi,
Mamadou-Saliou, tu ne précises pas à quel ensemble appartient n.
n appartient à Z, ou à N , ou à Z*, ou à N*, ou n est pair, ou n est impair ??? On n'en sait rien...
" montrer que les courbes (Cn) passent par trois points fixes" n'est pas bon pour tout n entier.
Nécessairement x > 0 : le Domaine de définition deFnF_nFn est ]0,+∞[]0,+\infty[]0,+∞[
Je te joins un schéma avec n prenant les valeurs entières comprises entre -5 et 5
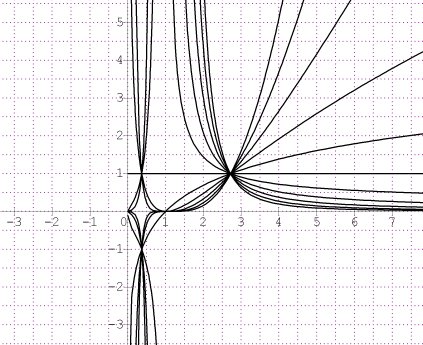
Pour n=0, Fn(x)=F0(x)=(lnx)0F_n(x)=F_0(x)=(lnx)^0Fn(x)=F0(x)=(lnx)0
000^000 est une forme indéterminée...
Donc pour x≠1x \ne 1 x=1 : F0(x)=1F_0(x)=1F0(x)=1 mais F0(1)F_0(1)F0(1) n'est pas défini
(on peut seulement faire un prolongement par continuité, ce que fait le schéma)Pour A(1,0) il faut imposer la condition n≠0n\ne 0n=0
ce n'est donc pas bon pour tout n entierPour B(e,1) c'est bon car pour tout n entier Fn(e)=(lne)n=1n=1F_n(e)=(lne)^n=1^n=1Fn(e)=(lne)n=1n=1
Pour C(1/e,-1) ce n'est pas bon pour tout n entier
Tout dépend de la parité de n
Fn(1e)=Fn(e−1)F_n(\frac{1}{e})=F_n(e^{-1})Fn(e1)=Fn(e−1)=[ln(e−1)]n=[−ln(e)]n=(−1)n[ln(e^{-1})]^n=[-ln(e)]^n=(-1)^n[ln(e−1)]n=[−ln(e)]n=(−1)n
Suivant la parité de n, Fn(1e)F_n(\frac{1}{e})Fn(e1) vaut +1 ou -1Donc, il faut être plus précis dans ton énoncé...
-
MMamadou Saliou dernière édition par
Bonsoir,
Je suis désolé pour le manque de précision et en réalité la fonction est x(lnx)^n donc la première fonction est une erreur
n: un entier non nul et x différent de zéro donc le domaine de définition (lR+) car Fn(0)=0
Merci !!
-
mtschoon dernière édition par mtschoon

Effectivement, cela explique pourquoi avec la première fonction que tu as donnée fn(x)=(lnx)nf_n(x)=(lnx)^nfn(x)=(lnx)n, il n'y ait pas 3 points fixes ! ! !
Avec les indications données précédemment, tu vas peut-être arriver à faire ton exercice.
Si j'ai bien compris, la "nouvelle" fonction est définie de deux façons :
Pour x > 0, Fn(x)=(lnx)nF_n(x)=(lnx)^nFn(x)=(lnx)n
Pour x=0, Fn(0)=0F_n(0)=0Fn(0)=0
Donc ainsi , FnF_nFn est définie sur [0,+∞[[0,+\infty[[0,+∞[Tu peux t'aider de ton graphique et tu trouveras cette fois 3 points fixes
Point (0,0) car Fn(0)=0F_n(0)=0Fn(0)=0
Point (1,0) et tu vérifies que Fn(1)=0F_n(1)=0Fn(1)=0
Point (e,e) et tu vérifies que Fn(e)=eF_n(e)=eFn(e)=ePour faire une démonstration mathématique ( pour retrouver les 3 points fixes et prouver qu'il n'y en a pas d'autres ), pour tout entier n non nul , tu peux résoudre l'équation
$\fbox{F_n(x)=F_{n+1}(x)}$ c'est à dire $\fbox{x(lnx)^n=x(lnx)^{n+1}}$Si besoin, tu peux donner tes calculs (avec la nouvelle fonction ) et nous vérifierons.