Exercice limite avec fonction E

Bonjour pouvez-vous m'aider dans mes réponses
Soit f une fonction défini par
{ $f (x) = x E (1 / x)$ ; $\lt 0$
{ $f(x)=(x−E(x))xf(x)=\dfrac{(x-E(x))}{\sqrt x}$ ; $x>0x\gt 0$

montrer que $f(x)=xf(x)=\sqrt x$ quel que soit $x$ de $] 0; 1 [$ puis déterminer $l i m f (x)$ en $0$ si $\gt 0$
2)est ce que la fonction $f$ ait une limite en $x_0=0$

Bonjour hafud,

Tu as combien d'exercices à faire ?
J'ai rectifié les fonctions, indique si cela est correct.

@Noemi oui c'est juste

@hafud

Je repose la question de Noemi :
Tu as combien d'exercices à faire ?
Merci d'y répondre et d'indiquer aussi si tu es scolarisé en lycée ou si tu travailles par correspondance, si tu prépares un Bac ou si tu fais une remise à niveau .

Je te démarre la 1) .
Il te suffit d'utiliser la définition de partie entière (regarde ton cours)

Danc cette question, x appartenant à ]0,1[ donc E(x)=0
donc $f(x)=x−0xf(x)=\dfrac{x-0}{\sqrt x}$

Il te reste à simplifier.

Essaie de poursuivre.

@mtschoon j'ai des séries d'exercices et je choisis les exercices difficile pour vous m'aider et je suis un lycéen

@hafud
D'accord.
Indique tes recherches sur la suite de cet exercice .
Nous vérifierons et te donnerons des indications si besoin, avec plaisir.

@mtschoon pour la première question j'ai fait
Soit $x$ appartient à $] 0; 1 [$
On a 0≤E(x)≤1
Donc $E (x) = 0$
Alors f(x)=x-0/√x=x/√x ×√x/√x=√x est ce que juste
Et comment il faut faire pour la limite

@hafud
Fais attention à la définition de partie entière
C'est sur [0,1[ que E(x)=0 (donc en particulier sur ]0,1[)
Pour la valeur 1, E(1)=1

Oui, sur ]0,1[, $f(x)=xf(x)=\sqrt x$ (ton calcul peut convenir)

Tu demandes " comment il faut faire pour la limite" ?

Réponse (évidente) :
Pour x>0, tu prends la limite $x\sqrt x$ , lorsque x tend vers 0
(ce sera la limite à droite de f)
Voici le réprésentation graphique le la fonction racine carrée.

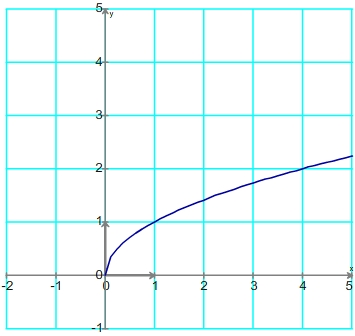
Tu étudies ensuite le cas x < 0

@mtschoon ah oui merci mais pourquoi on fait deux cas sur la limite

@hafud

Si tu as compris ma dernière réponse , commence par nous donner la limite de f lorsque x tend vers 0 par valeurs positives, c'est à dire la limite à droite en 0.
Je ne l'ai donnée car c'est à toi de la donner...
Tu as répondu "ah oui" mais tu ne donnes pas ta réponse...

Je t'ai écrit :
Pour x>0, tu prends la limite $x\sqrt x$ lorsque x tend vers 0
(ce sera la limite à droite de f)

Alors, quelle est la limite à droite de f en 0 ?

Ce sera seulement lorsque tu auras donner cette réponse qu'il faudra voir le cas x < 0.

@mtschoon 0

@hafud

Oui ! la limite à droite est bien 0

Pour répondre à la question 2), c'est à dire f a-t-elle une limite en 0 ?, il faut savoir si f peut avoir une limite à gauche en 0 égale à la limite à droite, c'est à dire 0 ( dans ce cas, on peut dire que f a une limite en 0).

Une idée possible, pour x < 0 (car chercher directement la limite n'est pas facile !)

Tu peux prendre une suite de valeurs de x de l'intervalle [-1,0[ qui tend vers 0 et chercher le comportement de f(x) pour ces valeurs
Soit $x=−1nx=\dfrac{-1}{n}$ , pour n appartenant à N*
Si tu explicites ces valeurs, x=-1, -1/2, -1/3, ...-1/1000, ....
(ces valeurs de x tendent vers 0 lorsque n tend vers $+∞+\infty$ )

$1x=−n\dfrac{1}{x}=-n$
$E(−1x)=−nE(\dfrac{-1}{x})=-n$
Donc
$f(x)=xE(−1x)=(−1n)×(−n)=+1f(x)=xE(\dfrac{-1}{x})=(\dfrac{-1}{n})\times (-n)=+1$

Conclusion : la limite à gauche en 0 de f ne peut pas valoir 0 vu que pour une suite de valeurs de x de [-1,0[ tendant vers 0, f(x) vaut constamment 1 (donc ne peut pas converger vers 0).

f n'a donc pas de limite en 0

@mtschoon c'est difficile a faire

@mtschoon a dit dans Exercice limite avec fonction E :

@hafud

Si tu as compris ma dernière réponse , commence par nous donner la limite de f lorsque x tend vers 0 par valeurs positives, c'est à dire la limite à droite en 0.
Je ne l'ai donnée car c'est à toi de la donner...
Tu as répondu "ah oui" mais tu ne donnes pas ta réponse...

Je t'ai écrit :
Pour x>0, tu prends la limite $x\sqrt x$ lorsque x tend vers 0
(ce sera la limite à droite de f)

Alors, quelle est la limite à droite de f en 0 ?

Ce sera seulement lorsque tu auras donner cette réponse qu'il faudra voir le cas x < 0.

Si on a E(x)=1 comment on trouve f(x)=√x je trouve (√x(x-1))/x

@hafud ,

Tu prends les choses à l'envers je pense...

L'énoncé te dit "montrer que $f(x)=xf(x)=\sqrt x$ quelque soit x de [0,1["
Donc sur l'intervalle [0,1[, x ne vaut pas 1 et E(x) ne vaut pas 1
C'est seulement sur l'intervalle [0,1[ que $f(x)=xf(x)=\sqrt x$
C'est cet intervalle qui est utile vu que l'on cherche ensuite le limite à droite en 0.

Remarque non demandée dans l'exercice, car elle ne sert pas pour la limite
E(x)=1 pour x appartenant à [1,2[
Sur cet intervalle [1,2[,
$f(x)=x−1x=x−1xf(x)=\dfrac{x-1}{\sqrt x}=\sqrt x-\dfrac{1}{\sqrt x }$

Autre remarque
Oui, l'étude pour x <0 est plus délicate.
D'ailleurs, regarde la formulation (subtile) de la question 2 :
l'énoncé ne te demande pas de chercher la limite à gauche en 0 mais seulement de chercher s'il y a une limite en 0.
Il suffit donc de prouver que 0, qui est la limite à droite, ne peut pas être la limite à gauche, d'où pas de limite en 0.

@mtschoon donc est ce que ma réponse est juste Pour 1

@hafud

Si tu parles de $f(x)=xf(x)=\sqrt x$ , oui c'est seulement par la question 1

@mtschoon oui merci et pour la deuxieme question j'utilise votre methode??

Pour la question 2)

Tu peux utiliser la méthode que je t'ai proposée (si tu n'en trouves pas d'autre, bien sûr)