Trigonométrie (aide) chasles

Bonsoiir j’ai un exercice en maths sur la trigonométrie c’est pour nous entraîner or j’ai vaiment du mal avec ce chapitre je ne sais jamais comment commencer.
Exercice:
On considere un triangle ABC, de sens direct, rectangle, isocèle et un triangle ADE, de sens direct, équilatéral tel que:
(Vecteur AC; VecteurAD)= pi/12 (2pi)
Demontrer que les droitesz (DE) et (BC) sont perpendiculaires.
J’ai commencé avec la relation de chasles en faisant (ce sont des vecteurs)
(AE;AD)=(AC;CB)+(CB;BA)+(BA;AE)+(AE;AD) (2pi)
Mais bon je ne suis pas sure car là je suis bloqué

Bonsoir shana67,

Calcule la mesure de l'angle (BC;DE)
Avec Charles
(BC;DE) = (BC;CA)+ (CA;AD) + (AD,DE)
= .....

Bonjour shana67 et bonjour Noemi,

@shana67 , un schéma pour éclairer le situation.

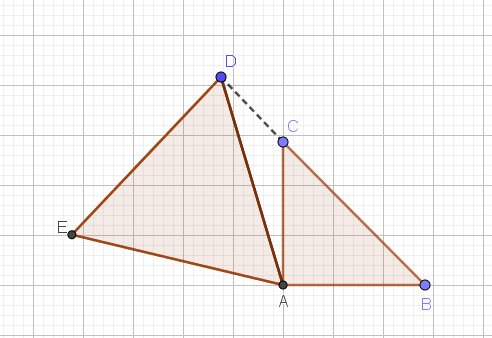
Un coup pousse pour avancer,

Utilise la relation donnée par Noemi, calcule chacun des 3 angles( à 2 $π\pi$ près) et fait la somme : tu doit trouver une mesure d'un angle droit

$(BC→,CA→)=(BC→,CB→)+(CB→,CA→)=π−π4=3π4(\overrightarrow{BC},\overrightarrow{CA})=( \overrightarrow{BC},\overrightarrow{CB})+(\overrightarrow{CB},\overrightarrow{CA})=\pi-\dfrac{\pi}{4}=\dfrac{3\pi}{4}$ ( $2π)2\pi)$

Continue.

@mtschoon
Bonsoir on fait comment pour calculer les angles ? À partir de celle donnée ?

@shana67

A partir des données de l'énoncé, tu peux écrire la mesure de tous les angles des triangles ABC, ADE.

@shana67

Comme déjà dit, utilise la relation de Chasles écrite par Noemi,

Je te calcule le second terme, de la même façon que le premier
(revois le)

$(CA→,AD→)=(CA→,AC→)+(AC→,AD→)=π+π12=13π12(\overrightarrow{CA},\overrightarrow{AD})=(\overrightarrow{CA},\overrightarrow{AC})+(\overrightarrow{AC},\overrightarrow{AD})=\pi+\dfrac{\pi}{12}=\dfrac{13\pi}{12}$ $(2π)(2\pi)$

IL te reste à calculer de la même manière le 3ème angle et ajouter.