Fonction dérivée et tangente

[omgabot]

Bonsoir,
Voilà le problème:
Soit f(x) = $a{x}^2$ + bx + c
On suppose que la courbe C représentative de f passe par les points A(0;1) et B(2;3).
Les tangentes T et T’respectivement de A et B se coupent en K(1;-4).
1-Déterminer f’(0) et f’(1).
Ma réponse:
f(x)=$a{x}^2$+bx+c
Donc f’(x)=2ax+b
Donc f’(0)=b
Et f’(1)=2a+b
2-Déterminé f’(x) en fonction de a et b.
C’est la où je comprend pas trop car j’y réponds en fait dans l première question:
f’(x)=2ax+b
Peut être faut-il que je réponde Eminem autre manière à la première question.
3-En déduire les valeurs de a,b et c.
Je suis actuellement en train d’y réfléchir.
Merci d’avoir pris le temps de lire

[Noemi]

Bonsoir omgabot,

Détermine pour la question 1, les équations des tangentes ou le coefficient directeur des tangentes.
$f^{\prime }(0)$ correspond au coefficient directeur de la tangente (AK).

Vérifie l'énoncé pour les coordonnées du point B ou pour f'(1) ?

[omgabot]

@Noemi
Merci de ta réponse en effet je trouve bien que f’(0) correspond bien au coefficients directeur de AK.
L’énoncé est correct moi non plus je comprend pas.Je pense que c’est une faute de frappe du professeur.
Par contre je comprend pas comment je peux déterminer f’(x) en fonction de a et b(question 2)
Je pensais faire la dérivée de f(x)=$a{x}^2$+bx+c
f’(x)=2ax+b??

[Noemi]

@omgabot

La dérivée est bien $f^{\prime }(x)=2ax+b$

Pour la question 3. Utilise $f^{\prime }(0)$ (pour trouver $b$), et les coordonnées des points A (pour trouver $c$)et les coordonnées du point B (pour trouver $a$).

[mtschoon]

Bonjour @omgabot et bonjour @Noemi ,

@omgabot , j'espère que tu as terminé tes calculs.

Je t'indique les valeurs à trouver pour que tu puisses vérifier les tiennes, si besoin.

$a=3,b=-5,c=1$, c'est à dire : $f(x)=3x^2-5x+1$

Je te joins le graphique pour contrôle de ces valeurs :

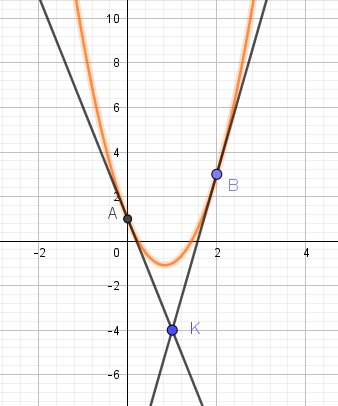
Bon travail.