Fonction : Intersection avec les axes. Etude. Tangentes.

Bonjour a tous
Je suis en train de faire un exercice sur les dérivés mais une question me pose probleme je n’arrive absolument pas a y repondre je ne sais pas par quoi commencer
Exercice
Soit f la fonction qui a x associe
$\dfrac{1,5x^2-4x+1}{2x+1}$
On me demande de determiner les coordonnées des points d´intersection de la courbe de f avec l’axe des absciesses et l’axe des ordonnes

Bonjour shana67,

Les points d'intersection de la courbe $C_f$ avec l'axe des abscisses sont tel que $f (x) = 0$ .
Les points d'intersection de la courbe $C_f$ axe l'axe des ordonnées ont pour abscisse $x = 0$ .
Pour la fonction, précise le numérateur de $2 x + 1$ .

@Noemi
Le numerateur c’est 1,5x^2-4x+1

Bonjour,

Je regarde un peu.

Tout d'abord, c'est bien d'indiquer sur quel ensemble on travaille.

La condition d'existence est
$\ne 0$ c'est à dire $x≠−12x\ne \dfrac{-1}{2}$
Donc $x∈x\in$ R / {-1/2}
Df=R / {-1/2}

Pour répondre à ta première question (intersection de la courbe avec l'axe des abscisses) :
f(x)=0 <=> $1,5x^2-4x+1=0$

Regarde ton cours sur les équations du second degré $ax^2+bx+c=0$ , en prenant ici a=1.5, b=-4 et c=1
Tu calcules $Δ\Delta$ puis les deux solutions de l'équation.

Une remarque : si l'énoncé donné est bien exact (vérifie), les solutions que tu obtiendras ne seront pas bien belles...

@mtschoon
Je trouve comme solution x=4-racine de10 /3
Et x2= 4+racine de 10/3
C’est ca?
Mais ducoup quelle est l’absCisse vu qu’on trouve 2 solutions ?

@shana67

Oui, il y a deux points d'intersection avec l'axe des abscisses.
Mets des parenthèses pour éviter les confusions.
x1=(4-racine de 10) /3 et x2=(4+racine de 10) /3

La courbe coupe l'axe des abscisses en deux points de coordonnées :
$(4−103,0)\biggl(\dfrac{4-\sqrt{10}}{3},0\biggl)$ et $(4+103,0)\biggl(\dfrac{4+\sqrt{10}}{3},0\biggl)$

Pour mieux visualiser, tu peux tracer la courbe sur ta calculette.
Si besoin, Je te mets une image.
Les points d'intersection de la courbe avec l'axe des abscisses sont A et B
Le point d'intersection de la courbe avec l'axe des ordonnées est C

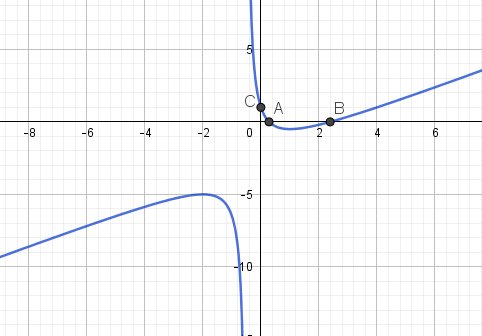
Il te reste à donner les coordonnées de C, intersection de la courbe avec l'axe des ordonnées

@mtschoon
La courbe coupe l’axe des ordonnes lorsque x=0 donc dans ma fonction je remplace x par 0 ?
(1,50-40+1)/2*0+1

Oui.

Mets suffisamment de parenthèses...
f(0)=(1.5 * 0² - 4 * 0+1)/(2 * 0 + 1)

En Latex
$f(0)=1.5×02−4×0+12×0+1f(0)=\dfrac{1.5\times 0^2-4\times 0+1}{2\times 0+1}$

Indique ce que tu obtiens.

@mtschoon
J’obtiens f(0)=1

Oui.

Les coordonnées de C sont donc $(0, 1)$

@mtschoon
Super merci beaucoup !
j’ai juste Une question concernant la suite de l’exo ou on me demande d’etudier les variations de f et de dresser le tableau de variation de f ( les valeur des extremums locaux sont attendus)
Donc en m’aidant de la dérivée 3x^2+3x-6 et en calculant delta (x1=-2 et x2=1) je trouve que la fonction est croissante puis decroissante et croissante a nouveau c’est juste?
Et en ayant comme extremums 0 pour f(-2) et f(1)

@shana67
Non mince je me suis trompé j’ai utilisé la dérivée pour les extremums du coup je trouve f(-2)= -5 et f(1)=-0,5

Il faudrait déjà savoir ce que tu trouves pour f'(x)

@mtschoon
(3x^2+3x-6)/(2x+1)^2

C'est bon.

Sur Df, (2x+1)² > 0 donc f'(x) est du signe de 3x²+3x-6

Pour simplifier un peu, tu peux mettre 3 en facteur:

3x²+3x-6=3(x²+x-2)

Vu que 3 est positif, il te suffit de chercher le signe de x²+x-2

Tes réponses sont exactes en ce qui concerne les extréma
(-2,-5) et( 1,-0.5)

Dans le tableau de variations, n'oublie pas de mettre une double-barre pour x=-1/2 ( valeur interdite)

@mtschoon
Mes variations aussi sont justes ?

Tu peux vérifier le sens de variation avec la courbe que je t'ai donnée.

Tu dois trouver :
f croissante sur ]- $∞\infty$ , -2]
f décroissante sur [-2, -1/2[
f décroissante sur ]-1/2,1]
f croissante sur [1,+ $∞\infty$ [

@mtschoon
Oui c’est exactement ce que je trouve merci
Dsl de vous deranger a nouveau mais je veux etre sur que mon exercice est juste du coup pour la suite on me demande de determiner une equation de la tangente a la courbe de f a point d’abscisse -1
En utilisant la formule d’equation de la tangente y=f’(a)(x-a)+f(a)
J’obtiens a la fin y=-6x-12,5 c’est juste?
Ensuite on me demande de déterminer les abscisses des points de la courbe de f ou la tangente est parallèle a l´axe des abscisses
Donc lorsque f’(x)=0
J’ai résolu l’equation et je trouve 2 solutions -2 et 1
C’est juste?

Oui, tout ce que tu as indiqué dans ton dernier post est juste.

Bon DM !

@mtschoon
Merci de m´avoir aidé !

De rien @shana67 ,

Si maîtrises bien ton exercice, c'est parfait.