Trigonométrie Première S

Bonjour, j'ai un dm de math a faire je n'y arrive pas même avec mes camarades de classe nous avons beaucoup de mal Merci de votre aide
Merci d'avance !

La seul chose qui me parait juste de ce que j'ai fait c'est la question 1
les coordonnées du points A (2cos ( t x 2pi ) ; 2sin ( t x 2pi ) )

Nous reprenons le spirographe dont je vous ai montré l’animation en classe. Le petit cercle tourne sans
glisser à l’intérieur du grand, dans le sens trigonométrique. Les rayons des cercles sont 1 et 3 cm.
La première figure est la position de départ. La deuxième figure montre la disposition des objets après
le début du mouvement.
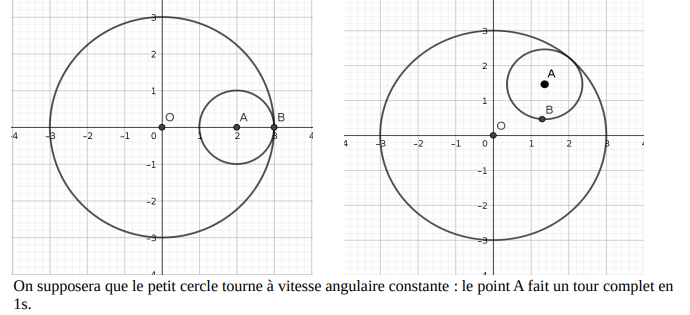
Capture f.PNG
On supposera que le petit cercle tourne à vitesse angulaire constante : le point A fait un tour complet en
1s.

Déterminer en fonction du temps t (en s) la position du point A.
Placez un nouveau repère d’origine A, avec des axes horizontaux et verticaux. Dans ce repère,
déterminez la position du point B.
INDICE :
Si C est le point de contact des deux cercles, la longueur d’arc parcourue par le point C sur le grand
cercle est égale à cette parcourue par le point B sur le petit
cercle, car les cercles ne glissent pas.
Attention ! Le point B tourne dans le sens antitrigonométrique !
En déduire la position du point B en fonction du temps.
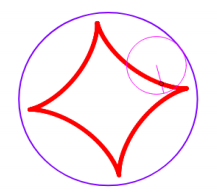
Avec ces rayons, voici la trajectoire du crayon :
Expliquez pourquoi au bout de 4 tours, le crayon est revenu à
sa position initiale.

Bonjour TaiZe,

Le scan de l'énoncé est interdit sur ce forum. Seuls les graphiques et schémas sont autorisés.
Recopie l'énoncé. Le scan va être supprimé.

@Noemi Je viens de remettre l'énoncé a était supprimé
Peut tu m'aider pour les question 3 et 4 j'ai reussie a faire les 2 premiers, Pour la question 1) A (2cos ( t x 2pi ) ; 2sin ( t x 2pi ) )
et pour la question 2 ) B(cos -2 x (2pi x t);sin -2 x (2pi x t))

@TaiZe

Pour la question 2, pourquoi -2 ?
Puisque le rayon du grand cercle est de 3 cm, pour un angle alpha, la longueur d'arc parcourue sur le petit cercle est de 3 alpha.

Pour la question 3, tu appliques $OB→=OA→+AB→\overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB}$ .

@Noemi car il faut prendre en compte le sens anti trigonométrique soit -3alpha + alpha qui nous donne -2 alpha

@TaiZe

Pourquoi +alpha, le point B part de la position (1; 0) et tourne de - 3 alpha.

@Noemi
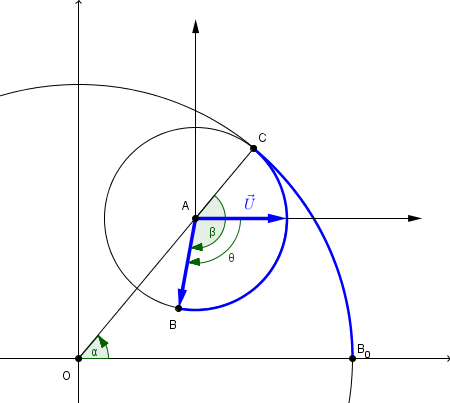
Il faut regarder dans cette figure, par définition les coordonnées de B dans le repère d'origine A sont (1cos(θ); 1sin(θ)), θ = -Beta+Alpha = -2 Alpha vu que Beta = 3Alpha

@TaiZe

Sur ton schéma, tu considères que le le point C correspond au point de départ de B (le $B_0$ ), ce qui n'est pas le cas, vu que le petit cercle tourne dans le sens antitrigonométrique. Donc il a tourné de -3 alpha.

@Noemi Oui c'est bien ce que j'ai dis, sur le sujet, le prof a bien mis que la longueur d'arc B0C = BC donc on peut en déduire l'angle Beta B0C = RxAlpha B0C = 3xAlpha Donc BC = 3Alpha x R Vu que R = 1 3Alpha = Beta

@TaiZe

Exact,
Le point B a tourné de - 3 alpha donc par rapport au repère cela donne - 2 alpha. C'est dans le cas de la position en fonction du temps qu'il faut prendre en compte -3 alpha.