Fonction et tableau de signe
-
MMelody dernière édition par
Bonjour j’ai cet exercice à faire mais j’en n’arrive pas à faire le tableau de signe..
G(x)= 3x3 -4x-8
La dérivée est 9x2-4 et ensuite il faut étudier les variations ce que j’ai fais
B) G(x)=0 admet une solution noté alpha
Et je dois déterminer le signe de g(x) selon les valeurs de x
Je n’arrive pas à trouver la reponse , merci de votre aide
-
Bonjour 2041,
Pour déterminer le signe de g(x)g(x)g(x) en fonction de xxx, il faut analyser les variations de la fonction à partir de son tableau de variations.
-
mtschoon dernière édition par

@2041 , bonjour
Si ton tableau de variation de G est exact, sur ]−∞,2/3]]-\infty,2/3]]−∞,2/3] , G(x)<0G(x) \lt 0G(x)<0
Sur ]2/3,+∞[]2/3,+\infty[]2/3,+∞[, G est continue et strictement croissante de G(2/3) (égal à -88/9) à +∞+\infty+∞
D'après de théorème des valeurs intermédiaires , il existe une valeur unique α\alphaα de ]2/3,+∞[]2/3,+\infty[]2/3,+∞[ telle que G(α)=0G(\alpha)=0G(α)=0
Donc
sur [2/3,α[[2/3,\alpha[[2/3,α[ , G(x)<0G(x)\lt 0G(x)<0
sur ]α,+∞[]\alpha,+\infty[]α,+∞[ , G(x)>0G(x)\gt 0G(x)>0Tu déduis ensuite le signe de G(x) sur R.
-
mtschoon dernière édition par

@Noemi , bonjour,
Je ne t'avais pas vu sur le forum et n'avais pas vu ta réponse...
-
MMelody dernière édition par
@mtschoon j’ai trouvé pour le tableau de variation -2/3 aussi comme solution
-
mtschoon dernière édition par

@2041
Tout à fait.
La dérivée s'annule pour -2/3 et 2/3
G(−2/3)=−569G(-2/3)=-\dfrac{56}{9}G(−2/3)=−956 et G(2/3)=−889G(2/3)=-\dfrac{88}{9}G(2/3)=−988
-
MMelody dernière édition par
@mtschoon d’accord merci!
-
mtschoon dernière édition par mtschoon

@2041 , de rien !
A toute fin utile, je te mets la représentation graphique de G pour vérification.
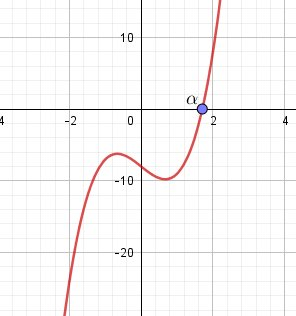
-
MMelody dernière édition par
@mtschoon cela permet de vérifier les variations , j’ai la même courbe sur la calculatrice donc ça doit être bon !
-
mtschoon dernière édition par

@2041 ,
Si ton tableau de variations correspond à la courbe, c'est bon !
Bon travail.