Fonction carrée définir sur R

Bonjour, je n’arrive pas à faire mon exercice voici son énoncé et ses questions.

Soit f la fonction carrée définie sur R par f(x)=x^2 et P la parabole la représentant dans un repère orthogonal du plan d'unité 1 cm sur l'axe des abscisses et 0,5 cm sur l'axe des ordonnées.

Question 1 : Tracer P.

Question 2 : Soit a un nombre réel, A le point d’abscisse a de P et Ta la tangente à P en son point A. Démontrer que l'équation de Ta est : y=2ax - a^2.

Question 3 : Soit B le point de coordonnées (2;1).
a)Tracer les éventuelles tangente à P passant par B.
b)Démontrer que la tangente Ta passe par le point B si, et seulement si, a^2-4a+1=0.
c)Résoudre l'équation (E):x^2-4x+1=0.
d)En déduire le nombre de tangente à P passant par B, en quels points elles sont tangentes à P et leurs equations.

Question 4 : Soit C le point deux coordonnées (1;2).
a)Conjecturer le nombre de droite passant par C et tangentes à P.
b)Démontrer que la tangente Ta passe par le point B si, et seulement si, a^2-2a+2=0.
c)Résoudre l'équation (F):x^2-2x+2=0.
d)Valider ou infirmer la conjecture est mise à la question 4-a

Merci d’avance pour votre aide.

Bonsoir rikiki72400,

Indique tes éléments de réponse et la question qui te pose problème.
Question 2, Si tu connais l'équation de la tangente en $x_0$ : $y = f'(x_0)(x-x_0) + f(x_0)$
tu peux écrire pour $x_0 = a$ : $y = 2a(x-a) + a^2$
Equation à simplifier.

Bonsoir @Noemi
Réponse question 1: J’ai réussi à faire la parabole P en faisant un tableau
F(x): -4 -3 -2 -1 0 1 2 3 4
x^2: 16 9 4 1 0 1 4 9 16

Réponse question 2 : on peut déterminer l’équation de la tangente à la parabole P en son point A d’abscisse quelconque a appartient au réel :
Pour tout réel h≠0,
f(a+h) - f(a)/h
= (a+h)^2 - (a)^2/h
= a^2 + 2 x a x h + h^2 - a^2 /h
= 2ah + h^2 /h
= h(2a + h) /h
= 2a + h
Or, lim h –> 0 (2a + h)= 2a
Donc la fonction carré de f est dérivable en tout réel a, et son nombre dérivé en a est f’(a)=2a.
L’équation réduite de la tangente à la parabole P en son point À d’abscisse a est :
y= f’(a)(x-a) + f(a) avec f’(a)= 2a et f(a)= a^2
Donc y= 2a(x-a) + a^2
<=> y= 2ax - a^2

Mais je n’arrive pas à tracer la tangente Ta sur ma parabole.
Voici le lien pour ma photo :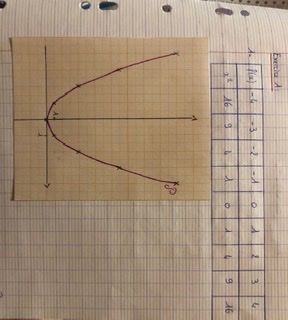
Après je suis bloquer à partir de la question 3.

@rikiki72400

3 a) Pour tracer les tangentes, tu places sur le graphique, le point B puis les tangentes.
b) Tu remplaces les coordonnées du point B dans l'équation de la tangente :
$1 = 4a - a^2$ d'ou l'équation .....
c) (E) Equation du second degré

@Noemi
3)a- voir photo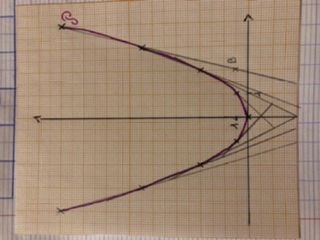

b- a^2 - 4a + 1 = 0
a^2 - 4a = -1
a^2 - 4a + (4/2)^2 = -1 + (4/2)^2
(a - 4/2)^2 = -1 + (4/2)^2
(a - 4/2)^2 = 3
(a - 2)^2 = 3
0 = -√3+2 ou 0 = √3+2
S= {-√3+2; √3+2}

c- E : x^2 - 2x + 2 = 0
x = -(-2)+ ou - √(-2)^2-4x1x2 / 2x1
x = 2 + ou - √(-2)^2-4x2 / 2
x = 2 + ou - √4-4x2 / 2
x = 2 + ou - √4-8 / 2
x = 2 + ou - √-4 / 2
x n’appartient pas au réel car la racine carre d’un nombre négatif n’existe pas dans l’ensemble des nombres réels.

d- Il y a qu’une tangente à P passant par B qui a pour équation 4x - 16.

@rikiki72400

a) Tu peux tracer deux tangentes passant par le point B.
b) Il faut retrouver l'équation en remplaçant $x$ par 2 et $y$ par 1
soit $1 = 4a - a^2$ équation que tu transformes .

c) Pour la résolution de $a^2-4a + 1 = 0$
Attention à la résolution Pourquoi écris tu $-\sqrt3 + 2$ ?
tu arrives à $a-2)^2 - 3 = 0$
si tu factorises cela donne $-\sqrt3)(a-2+\sqrt3)= 0$

d) Deux valeurs de $a$ possibles donc deux tangentes.
Pour trouver les coordonnées des points d'intersection de la tangente avec la fonction, il faut résoudre l'équation $x^2 = y$ .

@Noemi
a) je n’arrive pas à trouver l’autre tangente
b) si je remplace x par 2 et y par 1 l’équation est :(a x 2)^2 - 4a x 2 + 1 = 0
c) moi je trouve a = 2 −√3 ou a = 2 + √3. Comment vous trouvez (a -2 -√ 3) ou ( a-2+√3)

@rikiki72400

A partir de la factorisation :
$-\sqrt3)(a-2+\sqrt3)= 0$
tu déduis $\sqrt3$ et $\sqrt3$
On trouve deux valeurs pour $a$ , donc deux équations de tangente possibles.
Tu remplaces $a$ dans l'équation de la tangente $y = 2ax - a^2$ .

@Noemi
D’accord merci beaucoup de votre aide et de votre patience

@rikiki72400

Applique le même raisonnement pour la question 4.

@Noemi
D’accord merci

@rikiki72400

Une aide pour la dernière question.
a) Tu conjectures donc tu fais une hypothèse : par exemple "Aucune tangente possible"
b) Même démarche que la question 3
c) Pour la résolution, tu factorises $x^2 - 2x + 2 = (x-1)^2+1$
d) Tu valides ou non ton hypothèse.

@Noemi
A) il ne peut pas y avoir des droites passant par C et tangentes à P.
B) a^2-2a+2=0
a= -(-2)+ ou - √(-2)^2-4x1x2 / 2x1
a= 2 + ou - √4-4x2 / 2
a= 2 + ou - √-4 / 2
a n’appartient pas au Réel car la racine carrée d’un nombre négatif n’existe pas dans l’ensemble des nombres réels.
C) (F): x^2-2x+2=0
Même démarche et même résultat
x n’appartient pas au réel car la racine carre d’un nombre négatif n’existe pas dans l’ensemble des réels. Donc il n’y a pas de solution car l’équation est impossible.
D) je valide la conjecture que j’ai émise à la question 4-a.

@rikiki72400

Attention pour la question b) il faut démontrer comment on arrive à l'équation du second degré et non la résoudre.

Ce message a été supprimé !

@Noemi
D’accord donc du coup
a^2-2a+2=0
0 – 2 + 2 = 0
alors x = 0

@rikiki72400

Pour la question b) tu remplaces les coordonnées du point dans l'équation de la tangente.
Tu simplifies ensuite l'équation.

@Noemi
Coordonne du point C (1;2)
y=2ax−a^2
2= 2a1 - a^2
Donc maintenant je simplifie l’équation :
2 = 2a1 - a^2
2 = a^2 + 2a
a ( a + 2) = 2

@rikiki72400

Attention aux signes
$2 = 2a - a^2$ donne
$a^2 - 2a + 2 = 0$ équation qui est demandé.

Tu passes ensuite à la question c)
Résolution de l'équation : $x^2 - 2x + 2 = 0$
forme canonique : $x-1)^2+1 = 0$
or comme $(x−1)2≥0(x-1)^2 \geq 0$ et $1>01\gt0$ , alors $(x−1)2+1>0(x-1)^2 + 1 \gt0$
donc l'équation (F) n'a pas de solution dans l'ensemble des réels.