fonction carré et fonction cube-exercice 1
-
Ppouvens dernière édition par mtschoon
bonjour vous pouvez m'aider svp
comparer 0.2² et 0.3² ; puis (-0.2)² et (-0.3)² ; puis (−0.2)3(-0.2)^3(−0.2)3 et (−0.3)3(-0.3)^3(−0.3)3 (formules en puissance 3 re-écrites par la modération)
-
mtschoon dernière édition par mtschoon

@pouvens , bonjour,!
Tu dois connaître la fonction carrée définie par f(x)=x2f(x)=x^2f(x)=x2
Je te joins sa représentation graphique.
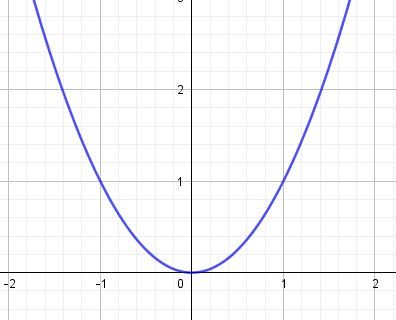
Pour x positif, elle est croissante donc
0.2<0.30.2 \lt 0.30.2<0.3 => (0.2)2<(0.3)2(0.2)^2\lt (0.3)^2(0.2)2<(0.3)2
(on élève au carré sans changer le sens de l'inégalité)Pour x négatif, elle est décroissante donc
−0.2>−0.3-0.2 \gt -0.3−0.2>−0.3=> (−0.2)2<(−0.3)2(-0.2)^2 \lt (-0.3)^2(−0.2)2<(−0.3)2
(on élève au carré en changeant le sens de l'inégalité)Je te joins la représentation graphique le la fonction cube définie par f(x)=x3f(x)=x^3f(x)=x3
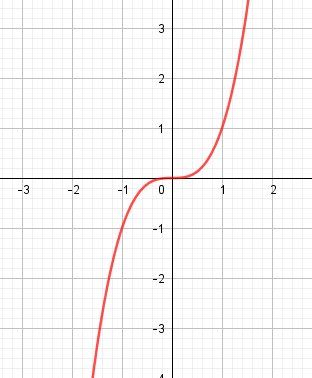
Elle est croissante sur R
On élève au cube sans changer le sens de l'inégalité
−0.2>−0.3-0.2 \gt -0.3−0.2>−0.3 => ...... (je te laisse compléter)
-
Ppouvens dernière édition par
pour la fonction carré c'est une parabole et la fonction cube ?
désolée c'est puis (-0.2)au cube et (-0.2)au cube donc c'est égale mais pourquoi
-
Bonsoir pouvens ,
La fonction définie par f(x)=x3f(x) = x^3f(x)=x3 est la fonction cube, pas d'autre nom.
Vérifie l'énoncé car (−0,2)3=(−0,2)3(-0,2)^3 = (-0,2)^3(−0,2)3=(−0,2)3
-
Ppouvens dernière édition par
oui c'est bien ça
(-0,2)^3 et (-0, 2)^3 c'est écrit comme ça
là il y a un espace mais je comprends pas
-
@pouvens
Donc tu notes l'égalité.
-
mtschoon dernière édition par mtschoon

@pouvens ,
Je reste perplexe.
Cet "espace"donc tu parles n'a pas de signification...
et (−0.2)3=(−0.2)3(-0.2)^3=(-0.2)^3(−0.2)3=(−0.2)3 est une"évidence" absolument sans aucun intérêt...(une lapalissade ! )Tu devrais demander des informations sur cette dernière question à ton professeur (ou tes camarades) car visiblement il y a une faute de frappe .
Pour dire quelque chose de cohérent :
Vu que la fonction cube est croissante sur R
−0.2>−0.3-0.2 \gt -0.3−0.2>−0.3 => (−0.2)3>(−0.3)3(-0.2)^3 \gt (-0.3)^3(−0.2)3>(−0.3)3
(on ne change pas le sens de l'inégalité en élevant au cube)
-
mtschoon dernière édition par mtschoon

@pouvens ,
Si ça peut t'être utile, je t'indique en complément, une synthèse relative aux fonctions croissantes et ou décroissantes sur un intervalle.
Si f est croissante sur un intervalle [a,b] de R
a≤x≤ba\le x \le ba≤x≤b <=> f(a)≤f(x)≤f(b)f(a)\le f(x) \le f(b)f(a)≤f(x)≤f(b)Si f est décroissante sur un intervalle [a,b] de R
a≤x≤ba\le x \le ba≤x≤b <=> f(a)≥f(x)≥f(b)f(a)\ge f(x) \ge f(b)f(a)≥f(x)≥f(b)Si tu préfères, cela revient au même d'écrire:
Si f est décroissante sur un intervalle [a,b] de R
a≤x≤ba\le x \le ba≤x≤b <=> f(b)≤f(x)≤f(a)f(b)\le f(x) \le f(a)f(b)≤f(x)≤f(a)
-
Ppouvens dernière édition par
merci beaucoup
-
mtschoon dernière édition par

De rien @pouvens,
Bon travail .