Fonction x -> g(x) et TVI

[Constance]

Bonjour !
J'ai un soucis avec mon exos...
Il y a des questions où j'ai besoin de vérification et d'autres d'aides..
Le voici,

On considère la fonction f définie sur R par f(x)= 4/(e^x)+1
On note C sa courbe représentative dans un repère orthonormé d'origine 0.

Partie A
On considère la fonction g définie sur R par g(x)= e^x - xe^x + 1

1. Calculer les limites de g(x) en + l'infinie et en - l'infinie
2. Étudier les variations de g. Dresser le tableau de variation de g.
3. Montrer que l'équation g(x)= 0 n'admet qu'une seule solution réelle a. Donner un encadrement de a d'amplitude 10^-2
4. Démontrer que e^a= 1/ a-1
5. Donner le signe de g(x) sur R

Pour la 1) j'ai trouvée - l'infini en + Infini
Et 0 en - l'infini

2. je pense avoir réussi..

3. celle-ci un gros blocage... J'ai essayé avec le TVI mais je n'y arrive pas

4. j'ai essayée de démontrer mais ça donner rien non plus

5. je crois que j'ai besoin des réponses aux réponses précédentes..

Merci!

[Noemi]

Bonjour Constance,

3. C'est bien le TVI,
   Utilises le tableau de variations, la partie ou la fonction décroit

4. Si $g(a)=0$ ; $e^a-a{e}^a=1=0$ ; équation à transformer.

5. Tu utilises le tableau de variations :
   Pour $x\in ]-\infty ;a]$ ; $g(x)......$
   pour $x\in ]a;+\infty [$ ; $g(x).......$

[mtschoon]

@Constance , bonjour, (et bonjour @Noemi )

@Constance, tu as écrit :
1) j'ai trouvée - l'infini en + Infini
Et 0 en - l'infini

En $+\infty$, la limite est bien $-\infty$ , mais en $-\infty$, ta limite est inexacte.

$\underset{x\to -\infty }{\lim }{e}^x=0$
$\underset{x\to -\infty }{\lim }x{e}^x=0$
Donc
$\underset{x\to -\infty }{\lim }(e^x-x{e}^x+1)=1$ c'est à dire
$\fbox{\displaystyle\lim_{x\to -\infty}g(x)=1}$

[mtschoon]

@Constance ,

Je t'indique les résultats de la 2) pour que tu puisses vérifier

Dérivée:
$g^{\prime }(x)=-x{e}^x$

Tableau de variation (disposition à améliorer car la flèche descendante n'est pas très claire dans mon tableau...)

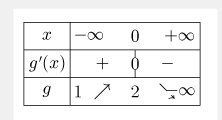
Pour les questions 3) 4) 5), suis les conseils de @Noemi .

Je te joins le graphique de g

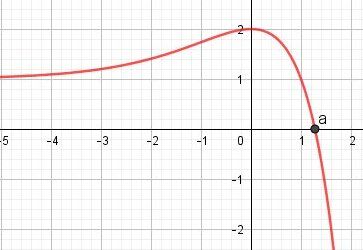
Reposte si besoin.

[Constance]

Merci beaucoup!