Dm sur les fonctions

Bonsoir , j’ai ce dm à rendre pour mardi et je comprend pas l’exercice pouvez vous m’aider svp.
Merci d’avance.

EXERCICE:

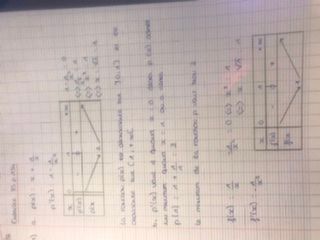
p est la fonction défini sur l’intervalle
]0;+♾[ par p(x)= x+1/x
a) étudier les variations de la fonction p
b)démontrer que le minimum de la fonction p sur l’intervalle ]0;+♾[ est égal à 3
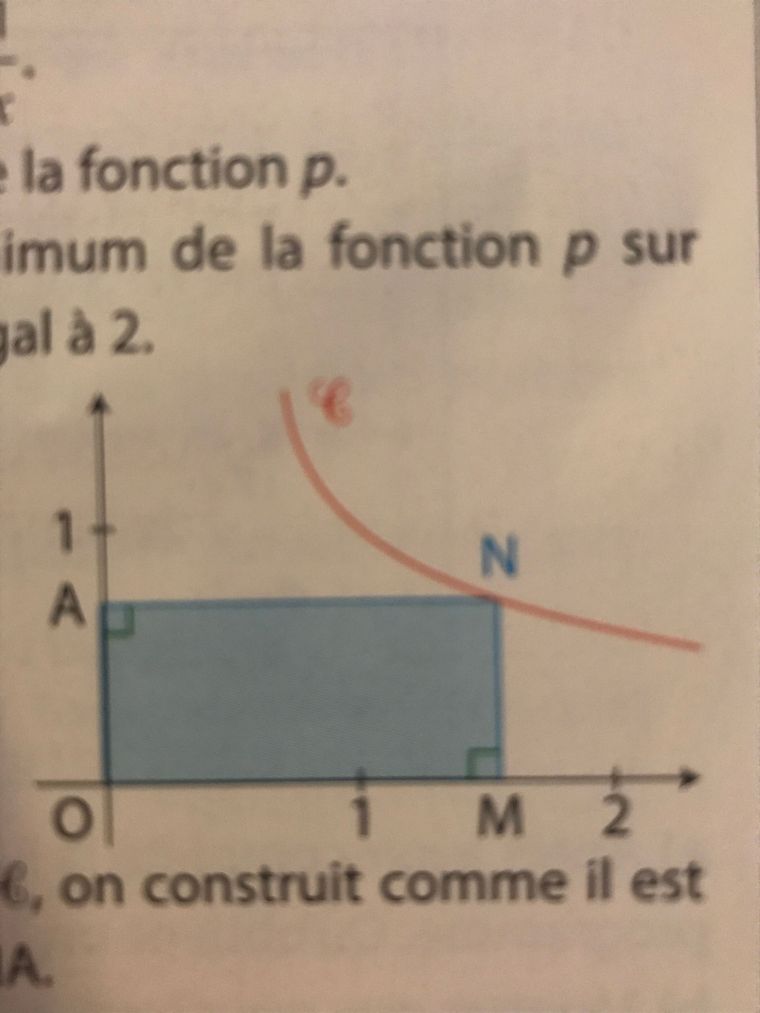
2.Sur la figure ci contre C est la courbe représentative de la fonction f définie sur ]0;+♾[ par : f(x)=1/x
A partir d’un point N de C, on construit comme il est indiqué le rectangle OMNA
Déterminer les dimensions du rectangle OMNA de périmètre minimum.

Bonsoir Ambrouux,

a) Calcule la dérivée soit $\dfrac{1}{x^2}$
Réduis au même dénominateur et étudie son signe sur l'intervalle ou la fonction est définie.

Le minimum vaut 2 ( et non 3).

@Noemi
Et pour la deuxième partie de l’exercice ?

@Ambrouux

Pour la fonction $f$ définie par $\dfrac{1}{x}$

Le périmètre $p_e$ du rectangle AMNO est : $pe=2x+2y=2x+2xp_e = 2x + 2y = 2x + \dfrac{2}{x}$

La fonction à étudier est : $pe(x)=2x+2x=2(x+1x)p_e(x) = 2x + \dfrac{2}{x} = 2(x + \dfrac{1}{x})$

Fonction à comparer avec celle étudiée à la question 1. Soit $p_e(x) = 2 p(x)$

@Noemi
Comment je réduis au même dénominateur ?
Comment vous avez trouvez que le minimum étais 2 ?

@Ambrouux

$\dfrac{1}{x^2} = \dfrac{x^2-1}{x^2}$ .
Résous $p^{'} (x) = 0$ puis dresse le tableau de variations.

Bonjour @Noemi et @Ambrouux ,

@Ambrouux , c'est bizarre...tu as posé des questions sur la partie 2 de ton Dm alors que tu ne sais pas faire la partie 1.
Il vaut mieux faire les questions dans l'ordre car parfois la réponse à une question sert à la question suivante.

Dans la partie 1, la fonction s'appelle p

Pour x > 0, $p(x)=x+1xp(x)=x+\dfrac{1}{x}$
On peut supposer que tu connais les dérivées usuelles , sinon il faut le dire.
Si c'est bien le cas, comme te l'a indiqué @Noemi ,
$p′(x)=1+(−1x2)=1−1x2=x2−1x2=(x−1)(x+1)x2p'(x)=1+\biggr(-\dfrac {1}{x^2}\biggr)=1-\dfrac{1}{x^2}=\dfrac{x^2-1}{x^2}=\dfrac{(x-1)(x+1)}{x^2}$

Pour $\gt 0$ , $x2>0x^2 \gt 0$ et $(x+1)>0(x+1)\gt 0$
La dérivée est donc du signe du numérateur $x - 1$
$\gt 0$ <=> $\gt 1$
$x - 1 = 0$ <=>... (tu complètes)
$x−1<0x-1\lt 0$ <=> ... (tu complètes)

Tu dois déduire que le minimum est pour x=1.
Pour $x =$ 1, $p(1)=1+11=....p(1)=1+\dfrac{1}{1}=....$ (tu complètes et tu trouveras ce que t'a indiqué Noemi.)

Tu dois obtenir un tableau de variations de ce type :

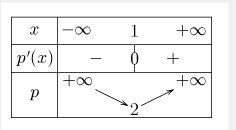
(J'ai indiqué les limites en 0 (par valeurs positives) et en $+∞+\infty$ , mais il ne faut peut-être pas les étudier car cela ne fait pas totalement partie des variations.
Vois en fonction de ton cours.

Reposte pour la suite si tu as besoin.

@mtschoon
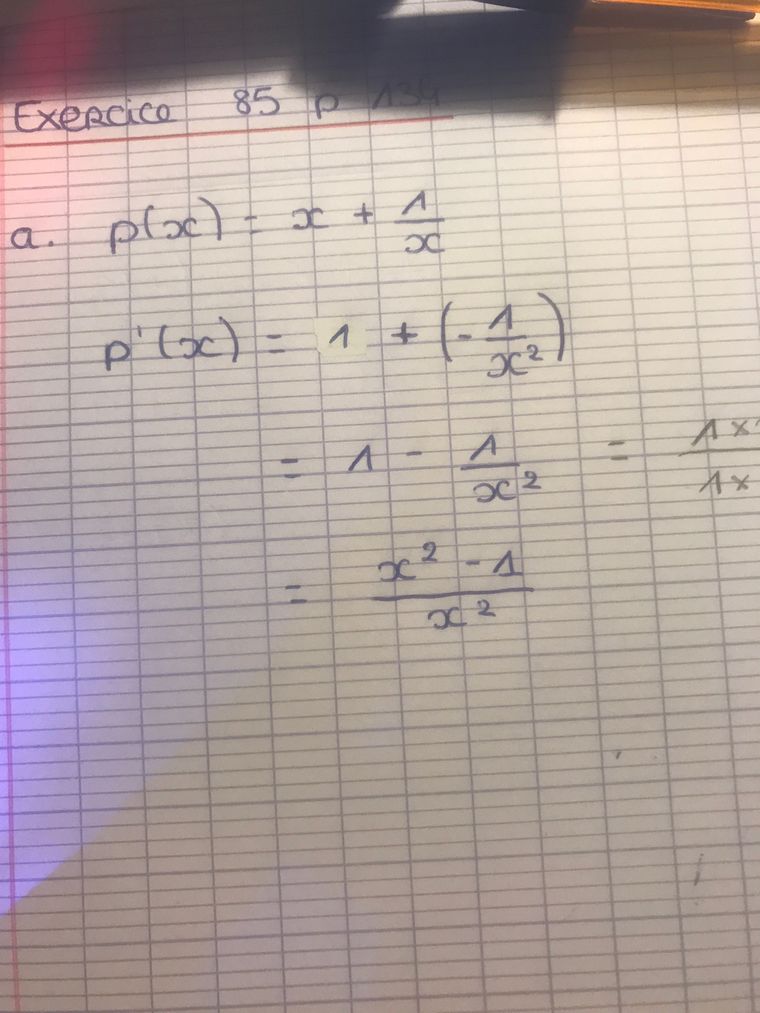
Je dois faire quoi après ça ?

@Ambrouux ,

Regarde la réponse de mtschoon, tu as la solution pour étudier les variations et déterminer le minimum.
Il suffit de compléter les pointillés.

@Ambrouux ,

Regarde ma réponse (pour l'aide à la partie 1)
Ce n'est pas la peine de poser des questions si tu ne regardes pas les réponses...

@mtschoon
Je pense avoir finis avec l’aide d’un de mes camarades j’espère que c’est bon

@mtschoon

@Ambrouux

La réponse à la question 2 est fausse. Tu n'as pas pris en compte les éléments de réponse indiqués.

@Noemi et @Ambrouux bonjour,

@Ambrouux , je te déconseille de scanner tes papiers.
Personnellement, je ne vois pas ce qu'il y a d'écrit et je ne peux pas te dire si c'est juste ou faux.
Fais comme tous les demandeurs : écris avec ton clavier.
Vu ce que dit @Noemi pour ta partie 2), ta réponse à cette partie 2) doit être à revoir.

J'explicite quelques pistes pour cette partie 2, si besoin.

(C) est la représentation graphique de f définie par $f(x)=1xf(x)=\dfrac{1}{x}$ , pour $x>0x\gt 0$
N est un point de (C) de coordonnées $(x, f (x)$ ) c'est à dire $(x,1x)(x,\dfrac{1}{x})$

Donc : $O M = A N = x$ et $MN=OA=1xMN=OA=\dfrac{1}{x}$

Le périmètre du rectangle AMNA est :
$O M + M N + N A + O A = 2 O M + 2 O A$
c'est à dire : $2x+2(1x)=2(x+1x)2x+2(\dfrac{1}{x})=2\biggr(x+\dfrac{1}{x}\biggr)$

J'appelle g(x) ce périmètre : $g(x)=2(x+1x)=2p(x)g(x)=2\biggr(x+\dfrac{1}{x}\biggr)=\fbox{2p(x)}$ , $p$ étant la fonction étudiée dans la partie 1 de ton exercice.

Vu que 2 est positif, Le sens de variation de g est le même que celui de p.
Tu n'as rien à faire .
Le minimum de g(x) est donc pour x=1
Ce minimum vaut $g(1)=2p(1)=2×2=4g(1)=2p(1)=2\times 2=4$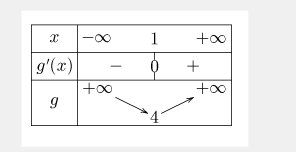

Il te reste à tirer la conclusion sur les dimensions de ce rectangle et tu verras que dans ce cas, le rectangle devient carré.

Regarde tout ça de près.