exercice mathématiques produit scalaire

Bonjour, j'ai de nombreuses exercices à faire pour la rentrée et l'un d'entre eux est sur le produit scalaire mais je bloque complètement et le cours ne nous a pas encore été distribué, je dispose que de quelques formules....

Exercice:
Soit ABCD un losange tel que AC = 8 et BD = 10. On note O le centre de ce losange.

Faire une figure.
Calculer $AC→\overrightarrow{AC}$ · $BD→\overrightarrow{BD}$ , puis $BC→\overrightarrow{BC}$ · $BD→\overrightarrow{BD}$ et $AB→\overrightarrow{AB}$ · $AC→\overrightarrow{AC}$
a. Décomposer le vecteur $AB→\overrightarrow{AB}$ en fonction de $AD→\overrightarrow{AD}$ et $DB→\overrightarrow{DB}$

En déduire $AB→\overrightarrow{ AB}$ · $AD→\overrightarrow{AD}$

b. De la même façon calculer $BA→\overrightarrow {BA}$ . $BC→\overrightarrow{BC}$

Merci d'avance

(Formules re-écrites en Latex par la modération)

@leo04 , bonjour,

Je commence par joindre une figure

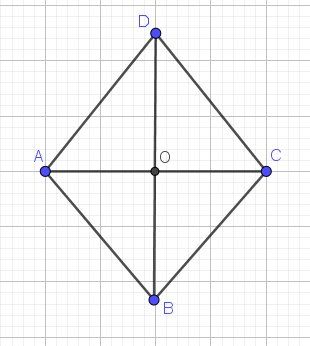
J'ai re-écrit les vecteurs de ton énoncé en Latex, car ce n'était pas clair...

@leo04 ,

Evidemment, tout dépend de ce que t'indique ton cours.

Je te donne des pistes pour commencer.

Les vecteurs $AC→\overrightarrow{AC}$ et $BD→\overrightarrow{BD}$ sont orthogonaux, donc leur produit scalaire est nul.

Avec la propriété relative à la projection,
$BC→.BD→=BO→.BD→=BO×BD×cos(0)=5×10×1=50\overrightarrow{BC}.\overrightarrow{BD}= \overrightarrow{BO}.\overrightarrow{BD}=BO \times BD\times cos(0)=5\times 10\times 1=50$

Essaie de poursuivre et tiens nous au courant.

okay merci

pour le premier calcul j'avais trouvé mais pour le deuxième je ne comprends pas, dans votre démarche, ce que devient le vecteur BC, pourquoi est-il égale à BO ?

Bonjour leo04,

C'est une propriété du produit scalaire correspondant à une projection orthogonale du vecteur $BC→\overrightarrow{BC}$ sur la droite $(B D)$ .
A voir avec le cours.

@leo04

$BO→\overrightarrow{BO}$ n'est pas égal à $BC→\overrightarrow{BC}$ .
Par projection orthogonale sur (BD), l'mage de B est B et l'image de C est O.

Si besoin, regarde ici, paragraphe III :
https://www.parfenoff.org/pdf/1re_S/geometrie/1re_S_proprietes_calcul_produit_scalaire_projete_orthogonal.pdf

Lorsque tu auras assimilé cette propriété, tu pourras l'utiliser pour le calcul de $AB→.AC→\overrightarrow{AB}.\overrightarrow{AC}$
Donne ta réponse à ce calcul si tu souhaites une vérification.

Bonjour, pour le deuxième je trouve 50 et enfin pour le troisième faut-il faire : (AO+OB) donc 0 . AC ?

Bonjour leo04,

Pour la question 2.
Le résultat des deux premiers produits scalaires est 0 et 50 (Voir la réponse de mtschoon).
Pour le troisième $AB→.AC→=AO→.AC→=....\overrightarrow{AB}.\overrightarrow{AC}= \overrightarrow{AO}.\overrightarrow{AC}= ....$

@leo04 ,

Pour $AB→.AC→\overrightarrow{AB}.\overrightarrow{AC}$ , si c'est de celui dont tu parles,

En projetant orthogonalement sur (AC),
$AB→.AC→=AO→.AC→=AO×AC×cos(0)=....\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AO}.\overrightarrow{AC}=AO\times AC\times cos(0)=....$
(Complète)

Pour la question 3), commence par utiliser la relation de Chasles :
$AB→=AD→+DB→\overrightarrow{AB}=\overrightarrow{AD}+\overrightarrow{DB}$

Ensuite, tu remplaces $AB→\overrightarrow{AB}$ par la décomposition qui vient d'être faite :
$AB→.AD→=(AD→+DB→).AD→\overrightarrow{AB}.\overrightarrow{AD}=(\overrightarrow{AD}+\overrightarrow{DB}).\overrightarrow{AD}$
Tu développes et tu calcules.

mais pour la deuxième(BC.BD) vous avez vous même dit que c'est égale à 50...
et pour AB.AC je trouve 32, est-ce bon ?
Je regarde tout de suite la 3
Merci à vous deux en tout cas

@leo04 ,

Plus plus de clarté, je résume :

$AC→.BD→=0\overrightarrow{AC}.\overrightarrow{BD}=0$
$BC→.BD→=50\overrightarrow{BC}.\overrightarrow{BD}=50$
$AB→.AC→=32\overrightarrow{AB}.\overrightarrow{AC}=32$

Tiens nous au courant de ton avancée pour la question 3 si besoin.

C'est bon, c'est ce que j'avais trouvé. Je fais la 3 plus tard, merci

@leo04 ,

D'accord.

Bonjour, pour la question 3 petit a, je trouve (AD+DB).AD = AD.AD + DB.AD

Je sais que DB = 10 mais commebt trouver AD ?

@leo04 , bonjour,

L'égalité vectorielle est bien :
$(AD→+DB→).AD→=AD→.AD→+DB→.AD→(\overrightarrow{AD}+\overrightarrow{DB}).\overrightarrow{AD}=\overrightarrow{AD}.\overrightarrow{AD}+\overrightarrow{DB}.\overrightarrow{AD}$

$AD→.AD→=AD×AD×cos(0)=AD×AD=AD2\overrightarrow{AD}.\overrightarrow{AD}=AD\times AD\times cos(0)=AD\times AD=AD^2$

(Peut-être que ton cours t'indique, ou t'indiquera, que le carré scalaire d'un vecteur est le carré de sa norme)

Pour calculer $AD^2$ , utilise le théorème de Pythagore dans le triangle rectangle AOD

okay AD au carré = 41 donc : AD au carré + DB x AD x cos(0) = 41 + 10 x racine(41) x 1 ?

@leo04 ,

Oui, $AD^2=41$ est exact.

Par contre $DB→.AD→\overrightarrow{DB}.\overrightarrow{AD}$ que tu donnes est faux car les vecteurs ne sont pas colinéaires.

Tu dois utiliser le théorème de la projection, que tu as utilisé déjà deux fois dans cet exercice.

Oui mais j'ai du mal avec ce théorème, peut etre : DB. (AO+OD) = DB.AO + DB. OD = 10x5x1 ?

@leo04 ,

Il bien que tu l'assimile ce théorème..
En projetant sur (DB),
$DB→AD→=DB→.OD→=.............\overrightarrow{DB}\overrightarrow{AD}=\overrightarrow{DB}.\overrightarrow{OD}=.............$

En utilisant ce que tu as écrit , ça marche aussi vu que
$DB→.AO→=0\overrightarrow{DB}.\overrightarrow{AO}=0$ et tu trouves ainsi $DB→.OD→\overrightarrow{DB}.\overrightarrow{OD}$

Mais, en calculant $DB→.OD→\overrightarrow{DB}.\overrightarrow{OD}$ , tu as une erreur sur le cosinus
L'angle que fait $DB→\overrightarrow{DB}$ avec $OD→\overrightarrow{OD}$ n'est pas l'angle nul , mais il est plat (car les vecteurs sont de sens contraire)
$DB→.OD→=10×5×cos(π)=10×5×(−1)=−50\overrightarrow{DB}.\overrightarrow{OD}=10\times 5\times cos(\pi)=10\times 5\times (-1)=-50$

c'est ce que j'ai mis non ? = 50 ?

@leo04 ,

Ce n'est pas 50 mais -50 (ce produit scalaire est négatif)

oh oui je vois, merci donc AB. AD = -9 ?

@leo04 ,
OUI !
$DB→.AD→=−9\overrightarrow{DB}.\overrightarrow{AD}=-9$

Pour la question 3)b), comme te l'indique l'énoncé, tu utilises la même méthode.

okay je vais essayer, mais je reprends tout même depuis la relation de Chasles ?

@leo04,
Oui.
$BC→=BA→+AC→\overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{AC}$

Tu poursuis.

BA² + BA.AC et BA² = -41, le début est correct ?

non pardon 41

BA² est un carré .
Il ne peut pas être négatif !
$BA→2=BA2=41\overrightarrow{BA}^2=BA^2=41$

Oui, c'est bien 41

je trouve ensuite-32 pour BA.AC... c'est bon ?

@leo04

Oui , et la valeur du produit scalaire demandé est ainsi 41-32=9.

c'est bon, j'ai fini par comprendre. Merci beacoup c'est fini

@leo04 ,
C'est bien . Tu as bien travaillé !