Representation markovienne

Bonjour,
j'ai la représentation suivante:
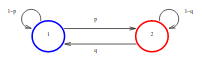
Capture du 2020-03-08 12-16-39.png

Comment calculer le temps moyen passé en 1, svp?

Bonjour lucky,

L'énoncé est complet ?

Bonjour Noemi,
Oui il est demandé de trouver le temps moyen passé en 1.
Sur internet j'ai trouvé 1/P (c'est un schéma assez courant) mais je ne vois pas comment arrivé à ce résultat

@lucky et @Noemi bonjour,

@lucky , je t'indique une interprétation possible à creuser , et à adapter si elle ne correspond pas à ton cours.

Evènement A : passer de l'état 1 à l'état 2 .
Probabilité P(A)=p

X : nombre d'épreuves répétées indépendantes jusqu'à ce que A soit réalisé pour la première fois.
X représente donc le temps passé à l'état 1 (avant de passer à l'état 2)

$P (X = 1) = P (A) = p$
$P(X=2)=p(Aˉ∩A)=(1−p)pP(X=2)=p(\bar A\cap A)=(1-p)p$
$P(X=3)=p(Aˉ∩Aˉ∩A)=(1−p)(1−p)p=(1−p)2pP(X=3)=p(\bar A\cap \bar A \cap A)=(1-p)(1-p)p=(1-p)^2p$
De façon générale
$P(X=n)=(1-p)^{n-1}p$

X suit la loi géométrique de paramètre p
Par théorème, son espérance (c'est le temps moyen que l'énoncé te demande ) est $1p\dfrac{1}{p}$

Evidemment, si cette propriété de l'espérance ne fait pas partie de ton cours, il faut la démontrer. Reposte si besoin.

C'est limpide. Merci vraiment merci

@lucky , de rien et bon travail!

Oups j'avais oublié de répondre merci

Mais si @lucky, tu avais déjà dit merci , mais c'est très gentil de le faire deux fois !

Bonne nuit.