Fonction usuelle et fonction inverse

[pouvens]

Bonjour vous pouvez m'aider svp
Résoudre l'inequation f(x)
1/x>2

[Noemi]

Bonjour pouvens,

Si l'inéquation est $\frac{1}{x}>2$
Pour $x>0$ cela donne $1>2x$
soit $x<......$

[pouvens]

@Noemi
Je dois donner l'intervalle
]0,0.5[

[Noemi]

@pouvens

Oui tu as
$x>0$ et $x<\frac{1}{2}$ donc $x\in ]0;\frac{1}{2}[$

[mtschoon]

Bonjour,

Si @pouvens travaille sur R, je suppose qu'il (elle) a réglé facilement le cas $x<0$
Pour $x<0$ , $\frac{1}{x}<0$, donc $\frac{1}{x}>2$ est impossible.

Autre version possible si @pouvens veut s'entraîner ( faute de cours en ce moment)
$\frac{1}{x}>2$<=> $\frac{1}{x}-2>0$

En réduisant au même dénominateur $\frac{1-2x}{x}>0$

En faisant le tableau de signes ( signe de $(1-2x)$, signe de $x$, signe de $\frac{1-2x}{x}$ ), on obtient :

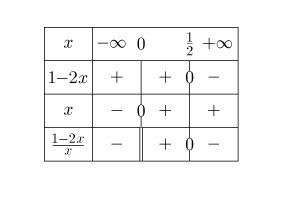
On retrouve ainsi que l'ensemble des solutions recherché est $]0,\frac{1}{2}]$

[pouvens]

ok merci

[mtschoon]

De rien @pouvens et bon travail !