Produit scalaire - géométrie

Bonjour,
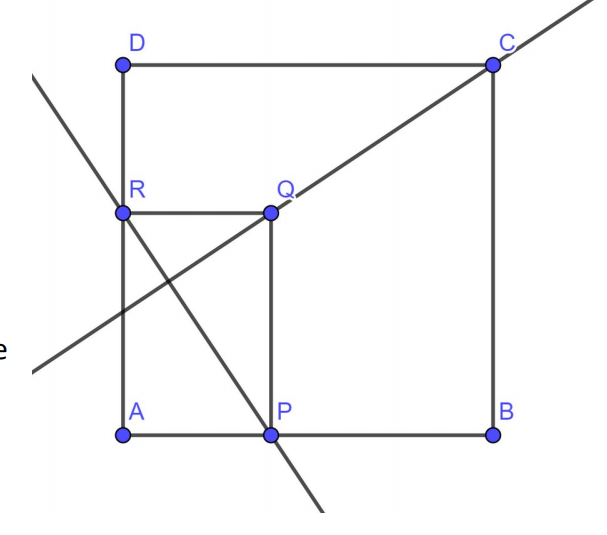
J'ai ces exo à faire mais je ne sais absolument pas comment faire ni par quoi commencer. Pouvez-vous m'aider ?

Soit ABCD un carré de coté a, et P un point du segment [AB]. On construit le rectangle APQR tel que :
R est un point du segment [AD] AP=RD
L’objectif de l’exercice est de montrer que les droites (CQ) et (PR) sont perpendiculaires.

Démontrer que le vecteur CQ . Le vecteur AR =−RD×AR . (on pourra utiliser la méthode de son choix, en expliquant )
a) Calculer le produit scalaire Vecteur CQ . Vecteur PR (penser à la relation de Chasles )
b) en déduire que les droites (CQ) et (PR) sont perpendiculaires.

Merci d'avance.

@enzo
Bonjour enzo,

C'est un exercice qui va te demander d'utiliser la méthode des projetés orthogonaux pour transformer le produit scalaire de gauche en celui de droite.

Mais tout d'abord, tu vas devoir décomposer astucieusement le vecteur $CQ→\overrightarrow{CQ}$ en utilisant la relation de Chasles.
Essaie quelque chose, et nous te dirons si tu es sur la bonne voie ou pas.

@Guillaume-87 Merci de ta réponse.
Je pense qu'on peut décomposer le vecteur CQ en faisant CAxAQ et après le relier a AR.

@enzo
Alors déjà, fais attention à la relation de Chasles : elle ne permet de décomposer des vecteurs "qui se suivent" qu'en utilisant une addition.
Donc tu aurais plutôt $CQ→=CA→+AQ→\overrightarrow{CQ} = \overrightarrow{CA}+\overrightarrow{AQ}$

Bon, mais maintenant il faut que tu choisisses bien ta décomposition, celle que tu as choisie ne sera pas très pratique.

L'astuce est de choisir une décomposition de $CQ→\overrightarrow{CQ}$ dans laquelle un des deux vecteurs sera orthogonal à $AR→\overrightarrow{AR}$ . Pourquoi ? Parce que de cette manière, quand tu développeras ton produit scalaire avec cette décomposition, tu auras un des produits scalaires qui sera égal à 0 : et cela est bien pratique, car ça permet de simplifier grandement le calcul !

Essaie de trouver une décomposition de $CQ→\overrightarrow{CQ}$ qui contient un vecteur orthogonal à $AR→\overrightarrow{AR}$ .

Je dirais que Vecteur CQ = Vecteur CD +Vecteur DQ. De cette manière le vecteur CD est orthogonal au vecteur AR.

@enzo
Et bien ça marche tout à fait convenablement, tu as bien compris l'astuce c'est très bien !
Et sache que ta première décomposition (CQ=CR+RQ) était aussi bonne : le sens des vecteurs n'a pas d'importance, car tu pourras les changer plus tard dans tes calculs en rajoutant un signe moins.

Maintenant, sers-toi de cette décomposition pour transformer le calcul $CQ→⋅AR→\overrightarrow{CQ} \cdot \overrightarrow{AR}$ : développe-le et essaie de le simplifier au maximum.

@Guillaume-87
Donc sa fait CD + DQ . AR et si j'ai bien compris, vu que CD et AR sont orthogonaux, c'est égal a 0 et donc il ne reste plus que le vecteur DQ.

Bonsoir enzo,

$CQ→⋅AR→=(CD→+DQ→)⋅AR→=....\overrightarrow{CQ} \cdot \overrightarrow{AR} = (\overrightarrow{CD}+\overrightarrow{DQ}) \cdot \overrightarrow{AR} = ....$

@Noemi a dit dans Produit scalaire - géométrie :

CQ⋅AR=(CD+DQ)⋅AR= DQ
je voi pas comment on peut faire autrement.

Il faut développer.
$CQ→⋅AR→=(CD→+DQ→)⋅AR→=CD→⋅AR→+DQ→⋅AR→=0+DQ→⋅AR→\overrightarrow{CQ} \cdot \overrightarrow{AR} = (\overrightarrow{CD}+\overrightarrow{DQ}) \cdot \overrightarrow{AR} = \overrightarrow{CD} \cdot \overrightarrow{AR} + \overrightarrow{DQ} \cdot \overrightarrow{AR} = 0 + \overrightarrow{DQ} \cdot \overrightarrow{AR}$
= ....

je suis dsl mais sa fait une demi heure que je cherche et j'ai vraiment pas trouver.

@Noemi je vois pas pourquoi ta mis 0+ dans la dernière partie.

Les deux vecteurs sont orthogonaux donc leur produit scalaire est ......

nul sa j'ai compris

@Noemi apres je pense qu'il faut décomposer DQ mais je sais pas comment.

Tu utilises une relation du cours sur le produit scalaire.

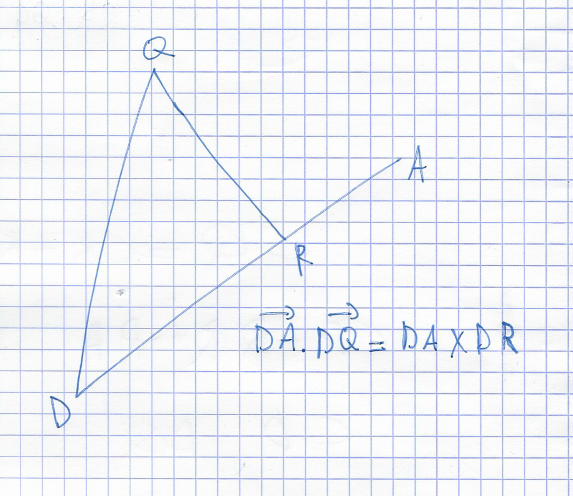
Sa ? @Noemi

Oui,

Tu peux utiliser cette relation.

Si on utilise cette relation, sa fait :

DA x DR =−RD×AR

Sa ne résous pas mon problème @Noemi

Je ne comprends pas la relation que tu as notée.

Tu dois calculer : $DQ→⋅AR→\overrightarrow{DQ} \cdot \overrightarrow{AR}$ .
Or par projection :
$DQ→⋅AR→=DR→⋅AR→=−RD→⋅AR→=.....\overrightarrow{DQ} \cdot \overrightarrow{AR} = \overrightarrow{DR} \cdot \overrightarrow{AR} =-\overrightarrow{RD} \cdot \overrightarrow{AR} = .....$

@Noemi On peut pas faire :

-vecteur RD . vecteur AR = -RD x AR ???

@enzo
Bonjour enzo,

Si ici on a le droit de le faire, pour la bonne raison que les vecteurs RD et AR sont colinéaires : autrement dit, leur produit scalaire est égal au produit de leurs longueurs, avec un signe moins si les vecteurs ont des sens opposés.

Ici RD et AR ont le même sens, donc on ne rajoute pas de signe moins, mais il y en avait déjà un présent dans l'expression, donc on le laisse. Autrement dit, par cette projection orthgonale que tu as très bien vue, on obtient la relation souhaitée.

Tu as compris, ça va ?

oui, c'est bon.
Par contre pour calculer CQ . PR , qui sera normalement egal a 0, je ne comprend pas comment on peut faire sachant qu'on a pas de mesure.

@enzo
Et bien il y a une petite astuce : c'est de comprendre que la question 1) était une étape préparatoire à la question 2). Sinon, pourquoi on te l'aurait posée, cette maudite question 1) ?

Tu dois donc répondre à la question 2)a) en utilisant exactement la même méthode que ce que tu as fait dans la 1), mais en prenant en compte ce paramètre : ta décomposition doit absolument faire apparaître, après développement, ce fameux produit scalaire $CQ→⋅AR→\overrightarrow{CQ}\cdot\overrightarrow{AR}$ , en plus d'un autre terme.

C'est sur cet autre terme qu'il faudra travailler dans cette question, pour aboutir au résultat $CQ→⋅PR→=0\overrightarrow{CQ}\cdot\overrightarrow{PR}=0$ comme tu l'as très bien compris.

Je te laisse déjà trouver la bonne décomposition.

@Guillaume-87 Je dirais :
PR= PA +AR
CQ= CA+AR + RQ
la je crois que c'est bien

@enzo
Presque. Ta première décomposition est impeccable, mais il ne faut pas décomposer $CQ→\overrightarrow{CQ}$ en deux vecteurs, sinon tu n'auras plus $CQ→\overrightarrow{CQ}$ dans ton développement et donc tu ne feras pas apparaître le produit scalaire de la première question.

Donc ne garde que la première décomposition, développe tout le produit scalaire et essaie d'aller le plus loin possible vers ce que tu dois démontrer.

PR= PA +AR
CQ= CA+AR + RQ
la je crois que c'est bien @Guillaume-87

@enzo
Heu tu viens de reposter le même message, enzo

oui je sais c'est parce que au debut j'avait poster une premiere decomposition a laquelle tu a repondu et apres j'ai éditer le message pour mettre une nouvelle décomposition et comme je savais pas si tu l'avais vu j'ai reposter le meme message. @Guillaume-87

@enzo
Ah d'accord.
Bon et bien tu as encore décomposé $CQ→\overrightarrow{CQ}$ , mais comme je te le disais il ne faut pas le décomposer du tout : il faut le garder tel quel, pour que dans le développement que l'on fera après, il soit encore présent pour qu'apparaisse le fameux produit scalaire $CQ→⋅AR→\overrightarrow{CQ}\cdot\overrightarrow{AR}$ .

On doit donc avoir :
$CQ→⋅PR→=CQ→⋅(PA→+AR→)\overrightarrow{CQ}\cdot\overrightarrow{PR}=\overrightarrow{CQ}\cdot \left(\overrightarrow{PA}+\overrightarrow{AR} \right)$

Développe ça, et essaie de te rapprocher le plus possible de ce que tu dois démontrer.

@Guillaume-87
CQ . ( PA + AR ) = CQxPA . CQxAR
Mais je comprendpas a quoi sa sert car rien n'est ortogonal.

Ce message a été supprimé !

@enzo
@enzo
Attention, ce n'est pas ce que l'on obtient ! Un produit scalaire se développe comme une multiplication, il suit les mêmes règles que la multiplication par rapport à une addition. Fais donc attention aux symboles :

$CQ→⋅(PA→+AR→)=CQ→⋅PA→+CQ→⋅AR→\overrightarrow{CQ}\cdot \left( \overrightarrow{PA} + \overrightarrow{AR} \right) = \overrightarrow{CQ}\cdot\overrightarrow{PA} + \overrightarrow{CQ}\cdot\overrightarrow{AR}$

Tu peux déjà remplacer $CQ→⋅AR→\overrightarrow{CQ}\cdot\overrightarrow{AR}$ par ce que tu as obtenu à la question 1), c'est la première chose à faire.

Ensuite il faut bien observer ta figure : en utilisant une projection orthogonale, ne pourrais-tu pas remplacer $CQ→\overrightarrow{CQ}$ par un vecteur qui serait plus pratique dans le produit scalaire $?→⋅PA→\overrightarrow{?}\cdot\overrightarrow{PA}$ ?

@enzo
Si tu ne trouves pas la bonne projection orthogonale,
il y a une autre méthode : c'est plus long mais comme tu le proposais plus haut, on peut aussi décomposer $CQ→\overrightarrow{CQ}$ dans le premier produit scalaire en passant par B, ou alors exactement comme tu le proposais (en passant par A et par R).
Dans ta décomposition par A et par R, d'ailleurs, il n'y aura pas de projection orthogonale mais uniquement des vecteurs orthogonaux et des vecteurs colinéaires.

@enzo
Allez, je vais t'aider encore un peu, car ce n'est peut-être pas très clair tout ça.

Le plus rapide est de créer le point $H$ , projeté orthogonal de $Q$ sur le segment $[C D]$ . Par définition, ABCD est un carré, APQR est un rectangle, et $(Q H)$ et $(C D)$ sont perpendiculaires. On en déuit donc que $(A B)$ et $(C D)$ sont parallèles, que $(P Q)$ et $(Q H)$ sont confondues et que la droite $(P H)$ ainsi formée est perpendiculaire à $(C D)$ et à $(A B)$ : on peut donc conclure que PBCH et APHD sont des rectangles.

Ainsi, on a :
$CQ→⋅PA→=CH→⋅PA→\overrightarrow{CQ}\cdot\overrightarrow{PA}=\overrightarrow{CH}\cdot\overrightarrow{PA}$ par projection orthogonale de Q sur [CD]
$CQ→⋅PA→=BP→⋅PA→\overrightarrow{CQ}\cdot\overrightarrow{PA}=\overrightarrow{BP}\cdot\overrightarrow{PA}$ car PBCH est un rectangle
$CQ→⋅PA→=BP×PA\boxed{\overrightarrow{CQ}\cdot\overrightarrow{PA}=BP \times PA}$

Voilà, maintenant tu n'as plus qu'à utiliser ce résultat pour l'intégrer dans ton calcul de $CQ→⋅PR→\overrightarrow{CQ}\cdot\overrightarrow{PR}$ , et tu devrais voir sans difficulté comment conclure maintenant.