calcul propabilité d'un schéma

Bonjour,
Je m'exerce à calculer les probabilités asymptomatique des états d'un schéma donné en fonction de p=0,6 et q =0.7
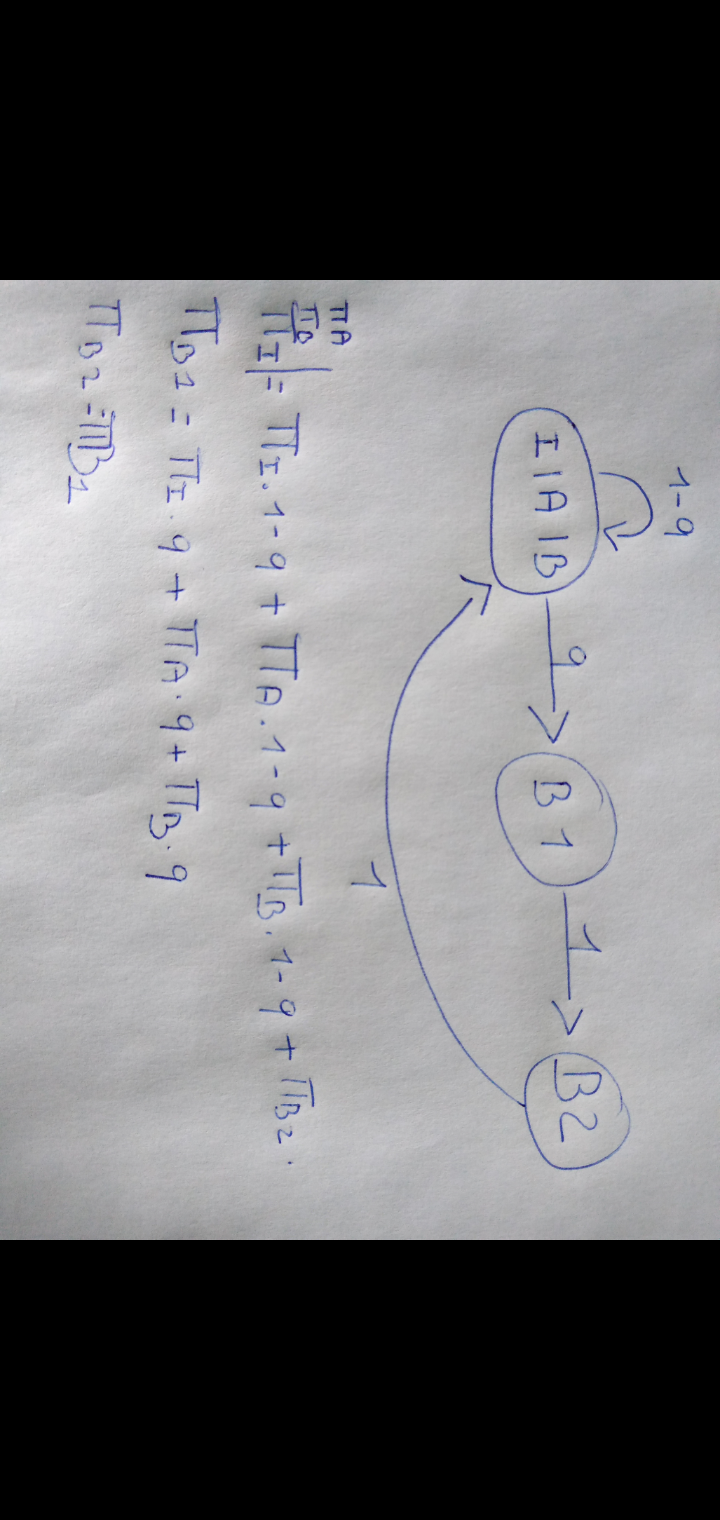
Puis il faut donner une interprétation numérique.

Je suis arrivé à écrire ça mais après je n'arrive plus à écrire.

Merci beaucoup

Bonjour flash38,

A quoi correspondent les valeurs de p et q ?

c'est juste des valeurs pour m’entraîner à calculer une fois que j'aurais calculé les probas des états

Bonjour,
Cela fait 2 jours que je tourne le problème dans tous les sens et je ne vois aucune solution possible.
Mon professeur me dit que c'est possible mais je ne comprends pas car j'ai trop d'inconnus dans chaque équation.

Quand pensez-vous?

Merci

@flash38 , bonjour,

Il est bizarre ton document...

Que signifie " probabilités asymptomatiques "?
Tu veux peut-être parler de" probabilités asymptotiques" , c'est à dire de recherche d'un état stable ?

Que signifie I | A | B dans le schéma ?

Que signifie
$πA∣\pi A |$
$πB∣\pi B |$ = dans ta première égalité ?
$∣\pi I\ |$

Tu parles de p et q alors que dans le schéma, il n'y a que q ...

Sans des explications rigoureuses sur ce qui est écrit , ce n'est guère possible de t'aider ...

Si tu as un énoncé, il serait souhaitable de l'écrire.

Bonjour,
Merci pour votre réponse.

Oui je veux bien parler de probabilités asymptotiques.
effectivement p n'est pas nécessaire.

Vu qu'il s'agit du même état j'ai mis A|B|I

L'énoncé sur lequel je me suis basé est:

Un chef de chantier dispose d’une seule équipe dont tous les membres travaillent sur le même chantier. Les demandes de travaux des clients qui lui parviennent peuvent être réparties en 2 catégories :

travaux de moyenne importance, durant une semaine (catégorie A).
travaux plus importants durant 3 semaines (catégorie B)

Les demandes de travaux parviennent au chef de chantier au début de chaque semaine. Une observation statistique a montré que les probabilités pour recevoir un lundi donné, au moins une demande de travaux de catégorie A, ou au moins une demande de travaux de catégorie B valent respectivement p= 0.6 et q= 0.7. Ces demandes arrivent de façon indépendante.Certaines semaines, des travaux sont refusés, l’équipe étant déjà occupée sur un chantier de caté B : dans ce cas le client s’adresse à un concurrent. D’autres semaines l’équipe reste inactive faute de demande. Si il est reçus simultanément 2 demandes : une de catégorie A et une de catégorie B, il donne systématiquement suite à celle de catégorie B.

Voilà j'espère que ça vous aidera à comprendre mon problème

@flash38 ,

Maintenant, tu donnes un énoncé sans question ...

Il serait bon d'écrire l'énoncé tel qu'il a été donné.

Je n'ai pas de question.

Le schéma donné plus haut a été modélisé grâce à cet énoncé.
J'essaie maintenant de calculer la probabilité de chaque état

@flash38 ,

Quelle histoire !

En regardant ton énoncé et le graphe que tu indiques , j'ai fini par comprendre (j'espère !), à peu près, de quoi il s'agit.

Je ne trouve pas que ton graphe illustre correctement le texte donné . Le nombre d'états n'est pas bon, et certaines probabilités non plus.

IL n'y a pas 4 états mais 5

Etat I : semaine inactive
Etat A : semaine où chantier A en activité
Etat B1 : semaine 1 où chantier B en activité
Etat B2 : semaine 2 où chantier B en activité
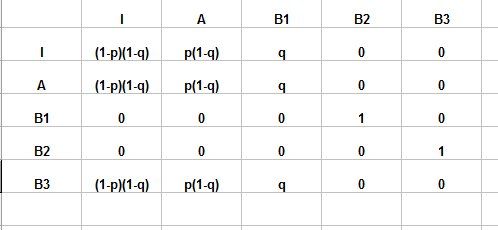
Etat B3 : semaine 3 où chantier B en activité

Je te mets un tableau (car plus facile à dessiner qu'un graphe)
En utilisant le tableau, tu peux mettre toutes ces données sous forme de graphe.

Légende du tableau :
La colonne à gauche correspond à une semaine n
La ligne en haut correspond à la semaine suivante (n+1)

J'ai calculé les probabilités en fonction de p et q mais bien sûr, tu peux mettre directement les valeurs numériques, en remplaçant p par 0.6 et q par 0.7

Dans tes équations, tu auras ainsi même nombre d'équations que d'inconnues en n'oubliant pas que la somme des probabilités vaut 1 (donc ça doit marcher).

Bonne réflexion.

Bonjour,
J'ai un peu le même problème qu'avant.
Si je regarde les 3 premières équations (I, A et B1) car B2et B3 =B1, par exemple pour I je ne peux pas résoudre l'équation car j'ai 2 inconnus dans l'équation: A et B3

@flash38 , bonjour,

Utilise le tableau et le fait que la somme des probabilités vaut 1

Merci pour votre réponse rapide.

Pour I j'ai comme équation:
I= I*(1-p)(1-q) + A*(1-p)(1-q)+ B3 (1-P)(1-q)
I- I*(1-p)(1-q) = A*(1-p)(1-q) + B3*(1-p)(1-q)

On est d'accord pour ça?
Si oui on est d'accord que je ne peux plus simplifier?

@flash38 ,

Nos réponses de sont croisées,
Il faut que tu raisonnes avec les 5 équations pas seulement sur 2.

@mtschoon Je ne vois rien de nouveau, j'ai bien vu votre égalité.

Mais quand j'essaie de résoudre I je ne retombe pas sur votre résultat et j'aimerais savoir ce que je fais mal

@flash38

Ecrit le système des 5 équations et observe le.

Alors comme système j'ai:
I = I*(1-p)(1-q) + A*(1-p)(1-q)+ B3 (1-P)(1-q)
A= Ip(1-q) + Ap(1-q)+ B3p(1-q)
B1= Iq + Aq+ B3q
B2=B1
B3=B2

quand je relis votre tableau pour moi c'est bien B3 pour I et non B1, je ne comprends pas

Merci pour ce que vous faite

@flash38

OK pour B1=B2 et B2=B3

Si une semaine il y a inactivité (I), la semaine suivante est ou bien en inactivité (I), ou bien en semaine A, ou bien en semaine B1 (car c'est la semaine 1 des grands travaux, si tu as utilisé les notations du tableau que je t'ai donné)

J'ai écris mes équations en fonction des flèches entrantes du schéma relatif au tableau. C'est peut être l'inverse donc ? les fleches sortantes?

@flash38

Regarde la tableau donné car un tableau me semble plus clair qu'un graphe où l'on peut se tromper en faisant les flèches.

Je crois que je viens de comprendre.
Je faisais mes équations en fonction des colonnes mais c'est en fonction des lignes qu'il fallait faire.

J'obtiens:
I= I*(1-p)(1-q) + Ap(1-q) + B1q
A= I*(1-p)(1-q) + Ap(1-q) + B1 * q
B1=B2
B2=B3
B3= I * (1-p)(1-q)+Ap(1-q)+B1 * q

Avec ces équations il est assez facile de voir que effectivement I=A=B1=B2=B3

@flash38 ,
C'est bien la colonne qu'il faut utiliser.
En utilisant I+A+B1+B2+B3=1, tu dois trouver les 5 valeurs

Je vais te chercher un site explicatif.

Merci beaucoup, c'est vraiment super ce que vous faites

@flash38 ,

Pour assimiler cet "état stable", tu peux consulter ici :
https://www.youtube.com/watch?v=PS756B-M0Dw

Bon travail à toi

Bonjour,

Calcul numérique en complément en prenant p=0.6 et q=0.7, comme indiqué dans l'énoncé.

Conformément au tableau fait précédemment, la matrice de passage M d'un état au suivant est , après calculs :
$0)\begin{pmatrix}0.12\ 0.18\ 0.7\ 0 \ 0\cr\ \ 0.12\ 0.18\ 0.7 \ 0 \ 0\ \ \cr\ \ \ \ 0\ \ \ \ 0\ \ \ \ \ 0\ \ \ 1\ \ \ 0\ \ \cr \ \ 0\ \ \ \ 0\ \ \ \ \ 0\ \ \ 0\ \ \ 1\cr 0.12\ 0.18 \ 0.7\ 0 \ \ 0 \end{pmatrix}$

Soit P la matrice-ligne décrivant l'état du système une semaine n
$P=(i,a,b_1,b_2,b_3)$

La matrice-ligne décrivant l'état du système la semaine (n+1) suivante est $P×MP\times M$

L'état stable du système vérifie $P×M=P\boxed{P\times M=P}$

D'où, après calculs
${0.12i+0.12a+0.12b3=i0.18i+0.18a+0.18b3=a0.7i+0.7a+0.7b3=b1b1=b2b2=b3\begin{cases}0.12i+0.12a+0.12b_3=i\cr 0.18i+0.18a+0.18b_3=a\cr0.7i+0.7a+0.7b_3=b_1\cr b_1=b_2\cr b_2=b_3\end{cases}$

Après transformations
${0.12(i+a+b3)=i0.18(i+a+b3)=a0.7(i+a+b3)=b1b1=b2=b3\begin{cases}0.12(i+a+b_3)=i\cr 0.18(i+a+b_3)=a\cr 0.7(i+a+b_3)=b_1\cr b_1=b_2=b_3\end{cases}$
d'où
${i0.12=a0.18=b10.7b1=b2=b3\begin{cases}\dfrac{i}{0.12}=\dfrac{a}{0.18}=\dfrac{b_1}{0.7}\cr b_1=b_2=b_3\end{cases}$

En calculant en fonction de $b_1$
${i=0.120.7b1a=0.180.7b1b2=b1b3=b1\begin{cases}i=\dfrac{0.12}{0.7}b_1\cr a=\dfrac{0.18}{0.7}b_1\cr b_2=b_1\cr b_3= b_1\end{cases}$

En substituant dans la formule fondamentale
$i+a+b_1+b_2+b_3=1$ ,
on obtient $b1=175618b_1=\dfrac{175}{618}$

Au final, après calculs , l'état stable du système est :

$P=(5103,15206,175618,175618,175618)P=\biggl(\dfrac{5}{103},\dfrac{15}{206},\dfrac{175}{618},\dfrac{175}{618},\dfrac{175}{618}\biggl)$

Bons calculs.