Résolution d'un système

Bonjour,

je me demandais comment pouvons nous déterminer l'ensemble des valeurs de a pour lesquels le système n'a PAS une unique solution. ( sous la forme d'un ensemble)

avec

(10+a)x+7y=8
-3x+ay=-2

merci d'avance pour votre aide !

@mimims , bonjour,

Le plus rapide est de calculer le déterminant principal du système (qui peut s'interpréter comme composé de deux équations de droites dans le plan)

$a∣D=\begin{vmatrix}10+a \ \ \ 7\cr -3\ \ \ \ \ \ a\end{vmatrix}$

$D=(10+a)a-(-3)7=a^2+10a+21$

Lorsque $D≠0D\ne 0$ , le système a un couple unique de solutions ( c'est le cas où les droites se coupent en un point)

Lorsque $D = 0$ , le système est impossible ou indéterminé (c'est le cas où les droites sont parallèles, distinctes ou confondues)

Bonjour@mtschoon,
Tout d'abord, merci pour votre réponse. Toutefois je me demande comment on trouve le déterminant principal d'un système ?

Bonjour mimims,

Le déterminant principal est constitué :
Première colonne, les coefficients de $x$ .
Deuxième colonne, les coefficients de $y$ .

Cette notion de déterminant principal n'est pas dans ton cours ?

@Noemi Non, je pense que c'est pour les élèves en spécialité mathématique.

Quelles méthodes connais-tu pour résoudre un système ?

Bonsoir,

@mimims , tu peux passer par les vecteurs directeurs des deux droites, et déterminer la condition pour que les vecteurs directeurs soient colinéaires ou pas .

Rappel si nécessaire :
Pour une droite d'équation Ax+By+C=0, un vecteur directeur a pour coordonnées (-B,A)

Ici:
$U→(−7,10+a)\overrightarrow{U}(-7, 10+a)$ et $V→(−a,−3)\overrightarrow{V}(-a, -3)$

Tu trouveras ainsi la condition que je t'ai indiquée.

Si besoin, tu peux revoir les vecteurs colinéaires ici, au paragraphe III:
https://www.mathforu.com/seconde/les-vecteurs-en-2nd/

Tu peux aussi trouver des éléments utiles ici ,
Il y a tout : vecteurs colinéaires et vecteur directeur d'une droite.
https://www.maths-et-tiques.fr/telech/VecteursDroites.pdf

Tiens -nous au courant si tu bloques.

@mimims ,

Pour plus de clarté, je résume.

Droite (D1) : (10+a)x+7y=8
$U→\overrightarrow{U}$ $(−710+a){-7}\choose{10+a}$

Droite (D2) : -3x+ay=-2
$V→\overrightarrow{V}$ $(−a−3){-a}\choose{-3}$

1er cas : $U→\overrightarrow{U}$ et $V→\overrightarrow{V}$ colinéaires.
$(- 7) (- 3) = (10 + a) (- a)$ <=> $a2+10a+21=0\boxed{a^2+10a+21=0}$

Equation du second degré à résoudre (tu dois trouver a=-3, a=-7)

Dans ce cas, (D1) et (D2) sont parallèles distinctes ou confondues.
Le système est impossible ou indéterminé

Tu peux faire le schéma des droites pour ces 2 valeurs de a pour t'en apercevoir.

2ème cas : $U→\overrightarrow{U}$ et $V→\overrightarrow{V}$ non colinéaires.
$(−7)(−3)≠(10+a)(−a)(-7)(-3)\ne(10+a)(-a)$ <=> $a2+10a+21≠0\boxed{a^2+10a+21\ne 0}$

a est différent de -3 et -7

Dans ce cas, (D1) et (D2) sont concourantes . Elles se coupent en un point I dont les coordonnées sont solutions du système.
Le système admet donc un couple de solutions.

Si tu veux avoir les valeurs des solutions, tu résous le système avec la méthode de ton choix.

CONCLUSION (réponse à ta question)
le système n'a PAS une unique solution dans le 1er cas traité , c'est à dire $\in$ { $- 3, - 7$ }

REMARQUE : Je t'ai indiqué les deux cas pour avoir une vue d'ensemble sur le sujet, mais pour répondre à la question de ton exercice, le 1er cas suffit.

Illustrations pour a=-3 et pour a=-7

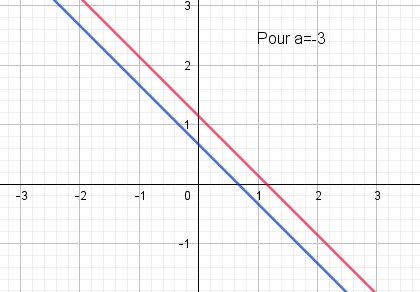
(sysème impossible)

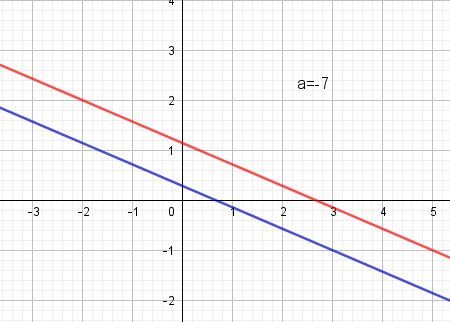
(système impossible)

@mtschoon merci beaucoup ! j'ai super bien compris !

@Noemi celle de la substitution et celle par combinaison

De rien @mimims .

Si tu as bien compris, c'est parfait.

Pour résoudre , tu connais, comme tu l'as indiqué à @Noemi, les deux méthodes usuelles mais ici, vu la question, tu n'avais pas besoin de résoudre le système.