Coordonnées d’un point

Bonjour à tous, j’espère que vous allez bien !
Je me dirige vers vous pour obtenir de l’aide, je ne sais pas comment faire et par quoi commencer. Merci de m’éclairer.

Énoncer : On considère A(6;1) et B(-3 ; 3) deux points du plan muni d’un repère orthonormé. Soit d la droite d’équation y= 2x + 3. Déterminer les coordonnées d’un point M appartenant à d tel que les droites (AM) et (BM) soient perpendiculaires.

Merci !

Bonjour Lisa-Martin,

Une méthode,
Tu peux rechercher une expression de l'équation de la droite $(A M)$ puis une expression de la droite $(B M)$
Tu utilises ensuite le fait qu'elle sont perpendiculaires et que le point d'intersection appartient à la droite $d$ .

Bonjour,

@Lisa-Martin ,

Si tu ne connais pas le produit scalaire, utilise la méthode proposée par @Noemi

Si tu connais le produit scalaire, tu peux te ramener directement à résoudre un système (avec équation du second degré)

A toute fin utile, je t'indique cette méthode
Soit M(x'y)
d'où $MA→(6−x,1−y)\overrightarrow{MA}(6-x,1-y)$ et $MB→(−3−x,3−y)\overrightarrow{MB}(-3-x,3-y)$

(AM) et (BM) perpendiculaires <=> $MA→.MB→=0\overrightarrow{MA}.\overrightarrow{MB}=0$

Cela équivaut à $(6 - x) (- 3 - x) + (1 - y) (3 - y) = 0$

En remplaçant y par 2x+3, tu obtiendras une équation du second degré d'inconnue x à résoudre.
Tu obtiendras deux solutions ( les abscisses des points d'intersection cherchés).
Avec y=2x+3, tu en déduiras les ordonnées.

Utilise la méthode qui correspond à tes connaissances.

Bonjour,

(6-x) (-3-x) + (1- 2x+3) (3- 2x+3)= 0

@Lisa-Martin ,

Je déduis que tu connais le produit scalaire.

Fais attention au signe lorsque tu remplaces y par 2x+3

$y = 2 x + 3$ donc $- y = - (2 x + 3) = - 2 x - 3$

L'équation s'écrit :
$(6 - x) (- 3 - x) + (1 - 2 x - 3) (3 - 2 x - 3) = 0$

Maintenant tu simplifies, tu développes et tu obtiendras une équation du second degré.

Donne tes résultats si tu as besoin d'une vérification.

@mtschoon

D’accord merci !

5x^2 + x - 10= 0 ?

@Lisa-Martin ,

Le "-10" est inexact.

Vérifie :

Tout d'abord, en réduisant, l'équation s'écrit

$(6 - x) (- 3 - x) + (- 2 x - 2) (- 2 x) = 0$

En développant et simplifiant, tu dois trouver:

$5x^2+x-18=0$

Donne les solutions si tu le souhaites.

@mtschoon

D’accord merci !
Du coup je calcule le discriminant :
1^2 - 4x5 x (-18) = 361
Donc deux solutions :

X1= -1 + Racine 361 / 2 x5 = 9/5

X2= -1 - Racine 361 / 2 x 5 = -2

Et après qu’est-ce que je dois faire ?

Calcule l'ordonnée de chacun des points en utilisant l'équation de la droite $d$ .

Je ne sais pas comment on doit faire

@Lisa-Martin ,

Oui, tes résultats pour les abscisses des points cherchés sont bons.

Vu que $y = 2 x + 3$ ,

pour $x=95x=\dfrac{9}{5}$ , tu obtiens $y=2(95)+3=...........y=2(\dfrac{9}{5})+3=...........$

pour $x = - 2$ , tu obtiens y=............

Donne tes résultats si tu le souhaites.

En complément, tu pourras , si ce n'est pas déjà fait, faire un graphique pour illustration/vérification.

Pour x = 9/5 y= 2(9/5) + 3 = 33/5

Pour x= -2 Y= 2x (-2) + 3 = -1

@Lisa-Martin

C'est bon.

Les points cherchés sont donc les points de coordonnées $(95,335)(\dfrac{9}{5},\dfrac{33}{5})$ et $(- 2, - 1)$

Revois toute la démarche de près pour être sûre de bien la maîtriser.

@Lisa-Martin ,

Pour illustration, je te mets un schéma.

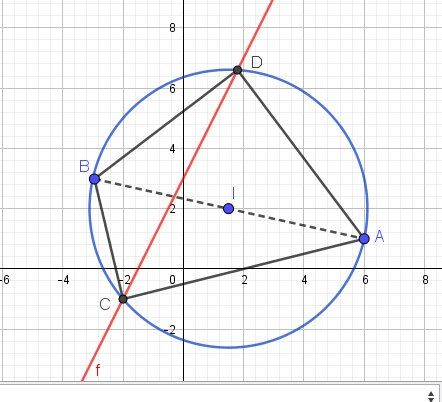
La droite (d) d'équation $y = 2 x + 3$ est en rouge

Vu que tu cherches les points M de (d) tels que l'angle $AMB^\widehat{AMB}$ est droit, ces points sont sur le cercle de diamètre [AB] (en bleu)

Les points cherchés sont dont les points C et D d'intersection de la droite rouge et du cercle bleu.

Tu peux ainsi vérifier que C a pour coordonnées $(- 2, - 1)$ et $D(95,335)D(\dfrac{9}{5},\dfrac{33}{5})$ c'est à dire $D (1.8, 6.6)$

Bon travail.

Ça marche merci bcp ! Mais le point M a 4 coordonnées du coup ?

@Lisa-Martin ,

Un point ne peut pas avoir 4 coordonnées !

Dans le plan, tout point a nécessairement deux coordonnées (abscisse, ordonnée).

Tu as dû mal t'exprimer.

Il y a DEUX positions de M qui conviennent, que j'ai appelé C et D sur le graphique que je t'ai donné.

En bref, M peut être placé en $C (- 2, - 1$ ) et aussi en $6.6)D(1.8\ ,\ 6.6)$

Si ces notations C et D ne te conviennent pas, tu les changes.

C peut être appelé $M_1$ de coordonnées $(- 2, - 1)$
D peut être appélé $M_2$ de coordonnées $6.6)(1.8\ ,\ 6.6)$

Bonnes réflexions.

Bonjour,

Presque la même chose ... mais sans traîner 2 variables dans les calculs.

M(X ; 2X+3) (puisque les points M appartiennent à la droite d'équation y = 2x+3)

vect(AM) = (X-6 ; 2X+2)
vect(BM) = (X+3 ; 2X)

vect(AM).vect(BM) = 0 (pour que les droites (BM) et (AM) soient orthogonales (et perpendiculaires puisque point M en commun))

(X-6).(X+3) + 2X(2X+2) = 0

X² - 3X - 18 + 4X² + 4X = 0
5X² + X - 18 = 0
X = -2 ou 1,8

M1(-2 ; -1)
M2(1,8 ; 6,6)

Merci à vous !!

Bonjour,

Personnellement, je préfère différencier les étapes pour que le demandeur comprenne mieux la démarche.

A chacun sa pédagogie !

Bonne journée.