exercice probabilité x désigne la population

[MOUNA8]

Bonsoir, j'ai des difficultés à résoudre la troisième question si je pourrais avoir des indications s'il vous plaît !

Un laboratoire pharmaceutique propose des tests de dépistage de diverses maladies. Son service de communication met en avant les caractéristiques suivantes :
la probabilité qu’une personne malade présente un test positif est 0,971 ;
la probabilité qu’une personne saine présente un test positif est 0,003.
Pour une maladie qui vient d’apparaître, le laboratoire élabore un nouveau test. Une étude statistique permet d’estimer que le pourcentage de personnes malades parmi la population d’une métropole est égal à 0,2%. On choisit au hasard une personne dans cette population et on lui fait subir le test.
On note :
M l’événement « la personne choisie est malade ».
S l’événement « la personne choisie est saine ».
P l’événement « le test est positif ».
N l’événement « le test est négatif ».
1.Traduire l’énoncé sous la forme d’un arbre pondéré.
2. Si le test est positif, quelle est la probabilité que la personne soit malade ?
3.Le laboratoire décide de commercialiser le test dès lors que la probabilité qu’une personne testée positivement soit malade est supérieure ou égale à 0,95. On désigne par x la proportion de personnes atteintes d'une certaine maladie dans la population. A partir de quelle valeur de x le laboratoire commercialise-t-il le test correspondant ? arrondir à 10^-3 près.

[Noemi]

Bonjour mimims,

Sachant que $P(M)=x$, écris la probabilité qu'une personne testée positivement soit malade en fonction de $x$.
Puis tu résous l'inéquation $P_T(M)\ge 0,95$.

[MOUNA8]

@Noemi D'accord merci je comprends je vais essayer de résoudre !

[mtschoon]

@mimims , bonjour,

Un petit plus si tu as besoin.

Si j'ai bien lu, P est l’événement « le test est positif ».

A la question 3), tu dois donc chercher

$\boxed{p_P(M)=\frac{p(M\cap P)}{p(P)}}$

Je pense que tu as fait un arbre, ou bien que tu as utilisé l'arbre de la première question en remplaçant 0.002 par x

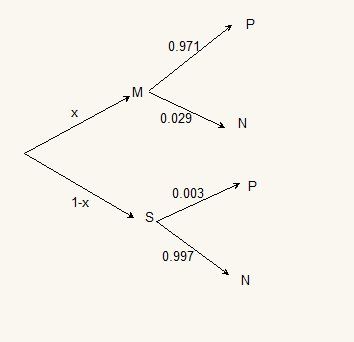
Avec l'arbre, tu peux tout calculer :

$p(P)=x\times 0.971+(1-x)\times 0.003$

$p(M\cap P)=x\times 0.971$

Tu dois donc résoudre
$\frac{x\times 0.971}{x\times 0.971+(1-x)\times 0.003}\ge 0.95$

Sauf erreur, x doit valoir environ 0.055 c'est à dire 5.5% (à vérifier)

Bons calculs .