Probabilités, pourcentages
-
Wil Fried dernière édition par Noemi

Bonsoir à tous! Besoin d'aide avec mon exercice svp.
Dans un train 20% des voyageurs portent un chapeau. 60% des voyageurs sont des femmes et 20% des hommes portent un chapeau. Quel est le pourcentage de femmes qui portent un chapeau ?
-
Bonsoir Wil-Fried,
Si 20% des voyageurs portent un chapeau et que 20% des hommes portent un chapeau, tu peux en déduire directement que ......
Tu peux vérifier en calculant comment se réparti le pourcentage de 20% de voyageurs qui portent un chapeau entre les hommes et les femmes.
-
Wil Fried dernière édition par

@Noemi Pourriez-vous me mettre sur la voie svp..
Je me retrouve pas vraiment.
-
@Wil-Fried
Quel est le pourcentage de voyageurs hommes ?
60% des voyageurs sont des femmes, donc ....
-
Wil Fried dernière édition par

@Noemi J'en déduis qu'il y a bien 40% de voyageurs hommes.
-
Wil Fried dernière édition par

@Wil-Fried Je trouve qu'il n'y a pas de femmes qui portent un chapeau. Aucune femme ne porte un chapeau. Parce que les 20% de voyageurs qui portent un chapeau sont en réalité les 20% d'hommes qui portent un chapeau. Du coup je trouve qu'il n'y aucune femme portant un chapeau.
-
Non,
Parmi les 40% de voyageurs hommes , 20% portent un chapeau,
ce qui donne en pourcentage ......Si les % te posent problème, suppose que le nombre de voyageurs est 100.
Tu as donc 60 voyageurs femmes et 40 voyageurs hommes.
Comme 20% des hommes portent un chapeau, cela donne .... hommes qui portent un chapeau.
Comme 20 voyageurs portent un chapeau, le nombre de femmes qui portent un chapeau est ....
Puis tu calcules le pourcentage de femmes qui portent un chapeau.
-
Wil Fried dernière édition par

@Noemi Je trouve 12femmes qui portent un chapeau.
En pourcentage on aura 12/60 = 20%
-
C'est juste.
-
Wil Fried dernière édition par

@Noemi Merciiii vous êtes géniaux


-
mtschoon dernière édition par mtschoon

Bonjour,
Maintenant que @Wil-Fried a bien compris son exercice, je me permets une réflexion..
L'exercice proposé était le cas trivial où 20% des voyageurs portent un chapeau et 20% des hommes portent un chapeau.
20% (voyageurs)=20%(hommes +femmes)
donc 20% (voyageurs)=20%(hommes) +20%(femmes)
Le pourcentage de femmes qui portent un chapeau était nécessairement 20%L'exercice serait différent si le pourcentage des voyageurs et le pourcentage des hommes n'étaient pas les mêmes.
-
mtschoon dernière édition par mtschoon

Pour lecture éventuelle, je complète ce exercice avec un cas non trivial où le pourcentage des voyageurs et le pourcentage des hommes ne sont pas les mêmes.
Par exemple :
Dans un train, 20% des voyageurs portent un chapeau. 60% des voyageurs sont des femmes et 15% des hommes portent un chapeau. Quel est le pourcentage de femmes qui portent un chapeau ?Version "probabiliste" vu que l'énoncé indique "exercice de probabilité"
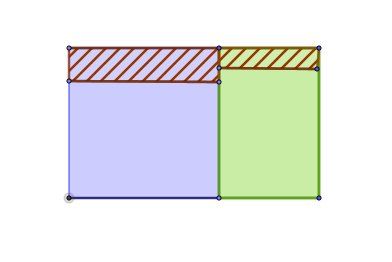
En bleu : ensemble F des femmes . p(F)=60p(F)=60p(F)=60%=0.6=0.6=0.6
En vert : ensemble H des hommes . p(H)=1−0.6=0.4p(H)=1-0.6=0.4p(H)=1−0.6=0.4
Hachures : ensemble C . p(C)=20p(C)=20p(C)=20%=0.2=0.2=0.2
CCC est composé de deux parties disjointes C∩FC\cap FC∩F et C∩HC\cap HC∩H
C=(C∩F)∪(C∩H)C=(C\cap F) \cup (C\cap H)C=(C∩F)∪(C∩H)
donc p(C)=p(C∩F)+p(C∩H)p(C)=p(C\cap F)+p(C\cap H)p(C)=p(C∩F)+p(C∩H)CALCULS
Probabilité des hommes portant un chapeau=pH(C)=15p_H(C)=15pH(C)=15%=0.15=0.15=0.15
p(C∩H)=pH(C)×p(H)=0.15×0.4=0.06p(C\cap H)=p_H(C)\times p(H)=0.15\times 0.4=0.06p(C∩H)=pH(C)×p(H)=0.15×0.4=0.06
donc p(C∩F)=p(C)−p(C∩H)=0.2−0.06=0.14p(C\cap F)=p(C)-p(C\cap H)=0.2-0.06=0.14p(C∩F)=p(C)−p(C∩H)=0.2−0.06=0.14Conclusion :
pF(C)=p(C∩F)p(F)=0.140.6=730p_F(C)=\dfrac{p(C\cap F)}{p(F)}=\dfrac{0.14}{0.6}=\dfrac{7}{30}pF(C)=p(F)p(C∩F)=0.60.14=307
pF(C)=0.233333.....p_F(C)=0.233333.....pF(C)=0.233333..... (infinité de 3)
Le pourcentage de femmes qui portent un chapeau est voisin de 23%Bonne lecture éventuelle.
-
Wil Fried dernière édition par

@mtschoon Merci beaucoup
-
mtschoon dernière édition par

De rien @Wil-Fried , et bonnes probabilités !