Exercice de probabilités casse-tête

Bonjour à tous !

Je viens vers vous car je sèche sur cet exercice :

Des tournois d'échecs sont organisés par une association :

Dans 70% des clubs (Clubs du nord : N), une partie entre deux joueurs consiste en 9 jeux. Chaque jeu est gagné par un des deux joueurs (il n'y a donc pas d'égalité).
Dans 30% des clubs (Clubs du sud : S), un match est gagné par le joueur qui arrive en premier à 6 jeux gagnés.

Et il est demandé de calculer la probabilité qu'un joueur ayant gagné 6-3 soit un membre des clubs du nord.

Dans toutes les possibilités ici, le joueur peut-être un joueur de club N vu qu'il y a 9 jeux joués au total.
Seulement faut-il tenir en compte le fait que le joueur ai pu passer de 6-2 à 6-3 (club N obligatoire) ou bien de 5-2 a 6-3 (club N ou S) ?

Je me trompe peut-être totalement, merci à vous.

Bonjour De-Perga,

Construis un arbre des probabilités avec les résultats possibles pour un match gagné. Puis tu étudies le cas 6-3.

Bonjour @Noemi ,

Est-ce que je dois partir du fait qu'il y a :

50% de chance qu'il y ait eu 6-2 avant d'arriver à 6-3 (ce qui me donne 100% de chance que le joueur soit du club N vu que sinon la partie se serait arrêtée avant 6-3 dans le cas du club S).
50% de chance qu'il y ait eu 5-3 avant d'arriver à 6-3 (ce qui fait que le joueur peut être du club N et S étant donné que dans les deux clubs il fallait arriver à 6-3 pour déterminer le vainqueur).

(Est-ce que je peux avancer ces pourcentages ? Vu que les seules informations, en terme de pourcentages, que j'ai sont sur le nombre de clubs).

Je coince sur la loi à utiliser du coup.

@De-Perga

Pourquoi 50% de chance ?

On part de la condition que le joueur a gagné.

@Noemi

Oui, je veux dire par là que la partie qui précède la dernière est déterminante afin de savoir si le joueur appartient au club N ou S non ?
(Je m'attache peut-être trop au contexte ?)
Je ne vois pas tellement quelles données utiliser mise à part le pourcentage des clubs.
Vraiment un exercice étrange, je n'arrive pas à trouver un exercice similaire étudié en cours...

@De-Perga

Tu pars des pourcentages puis tu écris les différentes possibilités ou un joueur gagne.

Pour le club du nord ; 5 possibilités soit (5-4; 6-3; 7-2; 8-1; 9-0) donc la probabilité pour 6-3 est .....
Pour le club du sud ; 6 possibilités soit .....

Je te laisse compléter les .... et conclure.

Indique tes résultats si tu souhaites une correction.

@Noemi

J'étais justement entrain de construire un arbre.
J'obtiens bien donc :

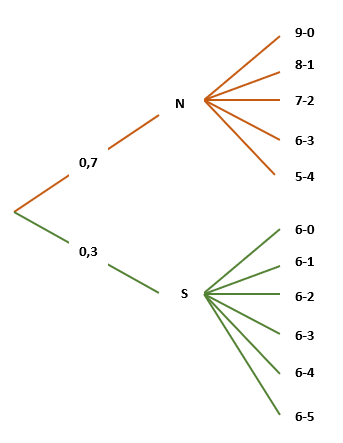
Vu que tu as dit qu'il y avait 5 et 6 possibilités j'imagine qu'on ne prends pas en compte l'inverse vu qu'on cherche que la victoire.
Est-ce qu'on admet qu'il y a autant de chance pour chaque score ? (Je sais pas si c'est utile de le savoir).

@De-Perga

C'est correct.
On peut admettre que dans une branche chaque score à la même probabilité.

@Noemi

Donc si j'admet que 6-3 (arbre du haut) est D. J'ai juste à calculer P(N|D) ?
J'ai utilisé Bayes :

P(N|D) = $P(D∣N).P(D)P(N)\dfrac{P(D|N).P(D)}{P(N)}$

Est-ce que P(D|N) = P(D).P(N) ?

Si oui, cela donnerait : P(N|D) = $(P(D).P(N)).P(D)P(N)\dfrac{(P(D).P(N)).P(D)}{P(N)}$ = $((0.2).(0.7)).(0.2)(0.7)\dfrac{((0.2).(0.7)).(0.2)}{(0.7)}$ = 0.04 = 4%.

Ce qui me semble impossible vu qu'il n'y a que deux possibilités : Club N ou Club S. Déjà les résultats devraient êtres complémentaires.

@De-Perga

Utilise :
$P_D(N)$ = $P(D∩N)P(D)\dfrac{P{(D\cap N)}}{P(D)}$

@Noemi

Ce qui donne du coup $P_D$ (N) = $P(D).P(N)P(D)\dfrac{P(D).P(N)}{P(D)}$ = $0.7$ = $7$ %
On revient donc au pourcentage que ce soit le club N, non ?
Seulement il est également possible que ce 6-3 soit dans un club S. Comment le prendre en compte ?

C'est énervant de pas arriver à comprendre !

@De-Perga

Non,
Pour $P (D)$ tu dois additionner la probabilité pour le club N et le club S, soit 0,14 + 0,05.
Pour $P(D∩N)P(D\cap N)$ c'est $0,7×0,2=...0,7\times 0,2 = ...$

@Noemi

Ah oui il faut prendre en compte le 6-3 du club S..

Donc on aurait $P_D$ (N) = $P(D).P(N)P(D)\dfrac{P(D).P(N)}{P(D)}$ = $P(D).P(N)PN(D)+PS(D)\dfrac{P(D).P(N)}{P_N(D)+P_S(D)}$ = $0.2∗0.7(0.2∗0.7)+(1/6∗0.3)\dfrac{0.2 * 0.7}{(0.2*0.7)+(1/6 *0.3)}$ ≈ $0.737 = 74$ %

Ce serait juste ? Maintenant ça me semble plus logique car je ne prenais pas en compte la totalité de la probabilité du 6-3 dans mon calcul.

Il y encore une chose qui défie ma logique. Dans l’énoncé de l'exercice, on sait dès le début que le joueur a remporté sa partie avec 6-3. Alors pourquoi prendre en compte d'autres scores ? C'est peut-être bête comme question mais j'arrive pas à me la sortir de la tête.

Il n'existerait pas une autre méthode avec une loi pour y arriver (type loi géométrique) ?

@Noemi a dit dans Exercice de probabilités casse-tête :

@De-Perga

Tu pars des pourcentages puis tu écris les différentes possibilités ou un joueur gagne.

Pour le club du nord ; 5 possibilités soit (5-4; 6-3; 7-2; 8-1; 9-0) donc la probabilité pour 6-3 est .....
Pour le club du sud ; 6 possibilités soit .....

Je te laisse compléter les .... et conclure.

Indique tes résultats si tu souhaites une correction.

Bonjour,

Ta réponse (club nord) sous-entend que la proba de faire (pour un joueur) un score de 5-4 est la même que celle de faire un score de 6-3 ou un score de 7-2 ou ...

Cela ne me semble pas du tout acquis, pour moi, les différents scores ne sont pas équiprobables, loin s'en faut.

Il me semble par exemple que la proba pour un joueur du score 9-0 est P(9;0) = 1 - (1 - 1/2^9) = 0,001953...
Et ceci en "oubliant" la qualité du joueur, sinon c'est inextricable.

Cette proba (0,001953) semble être confirmée par une simulation (j'ai simulé 140 fois 5000 parties de 9 jeux) et la moyenne du score 9-0 trouvé est 0,00195

A titre indicatif, la simulation donne une proba de 0,16 pour le score 6-3 (et pa

Bonjour,

Mon message précédent a été envoyé non terminé (fausse manoeuvre ?)

Je voulais poursuivre ainsi :

...
A titre indicatif, la simulation donne une proba de 0,16 pour le score 6-3 (et pareil pour le score 3-6)

Soit, je me trompe, soit non, et il reste possible que le prof ait aussi considéré (pour moi, à tort) tous les "scores" comme équiprobables et que donc la réponse soit alors celle préconisée.

Personnellement, je hais le calculs des probabilités.

Bonjour @Black-Jack et merci pour ta réponse !

Alors justement, j'ai posé la question au prof directement. Et il nous a dit que nous aurions besoin de la probabilité (p) que le joueur (dont l'on cherche l'appartenance à un des clubs) gagne un jeu. Il confirme donc que ce paramètre ne nous est pas indiqué et que nous le trouverions au cours de nos calculs..
Il nous dit ensuite que nous pouvons supposer que p=1/2 afin d'arriver au bon résultat.

Est-ce que cela signifie que notre démarché est la bonne ? Sinon je comprends totalement ton résonnement qui logique.

Et je n'éprouve également que très peu d'affection pour les probabilités aha !

@De-Perga

Si on ne considère pas que les cas sont équiprobables, il faut pour chaque branche de l'arbre, calculer le nombre de possibilités.

@Noemi
Et d'après toi que voulait dire mon prof par la probabilité qu'un joueur gagne un jeu = 1/2 ?

Est-ce que je doit pas tenir compte du jeu qui précède 6-3 ? (tel que dans l'arbre suivant) :

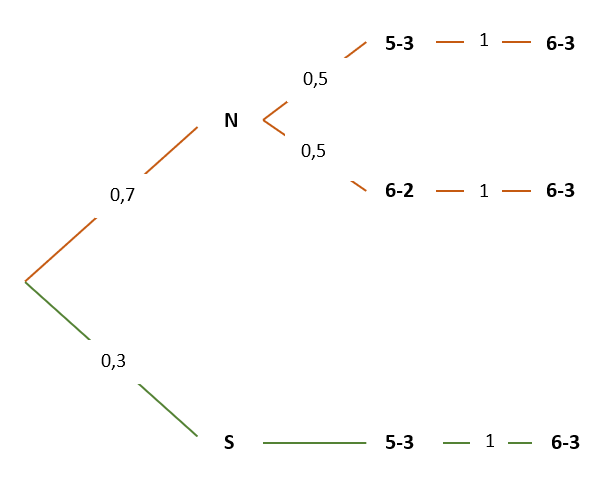
Au final je suis plus embrouillé qu'autre chose..

@De-Perga

D'après ce que tu as écrit. Ton professeur a indiqué que tu pouvais supposer que p = 1/2. Il est vrai qu'a chaque partie la probabilité de gain est de 1/2.
Il ne suffit pas de prendre le résultat précédent mais l'ensemble des résultats.
Pour le Nord, calcule pour chaque cas indiqué dans le premier arbre, le nombre de possibilités.

Rebonjour,

Si la proba de gagner 1 match est de 1/2

La proba de gagner exactement 6 fois en 9 matchs est C(9,6)/2^9 = 84/512 = 21/128 (0,1640625)

La proba d'un score (6-3) est donc 21/128 pour les joueurs d'un club du Nord

...

@Noemi

@Black-Jack a dit dans Exercice de probabilités casse-tête :

Ta réponse (club nord) sous-entend que la proba de faire (pour un joueur) un score de 5-4 est la même que celle de faire un score de 6-3 ou un score de 7-2 ou ...

Cela ne me semble pas du tout acquis, pour moi, les différents scores ne sont pas équiprobables, loin s'en faut.

Il me semble par exemple que la proba pour un joueur du score 9-0 est P(9;0) = 1 - (1 - 1/2^9) = 0,001953...
Et ceci en "oubliant" la qualité du joueur, sinon c'est inextricable.

Cette proba (0,001953) semble être confirmée par une simulation (j'ai simulé 140 fois 5000 parties de 9 jeux) et la moyenne du score 9-0 trouvé est 0,00195

A titre indicatif, la simulation donne une proba de 0,16 pour le score 6-3 (et pareil pour le score 3-6).

En effet, ça me semble logique que la probabilité que le joueur l'emporte avec 9-0 soit moins ''probable'' que de l'emporter avec 5-4 par exemple sans prendre en compte le niveau des joueurs (et donc que les différents scores ne soient pas équiprobables).

Je dois donc calculer, tel que Black-Jack, la probabilité que chaque score se réalise pour ensuite pouvoir modifier mon calcul de probabilité réalisé précédemment pour avoir une approche plus juste de la réalité ?

Cependant, pour ce qui est de la probabilité P(9-0) = 1 - (1 - 1/2^9) = 0,00195 : le 9 provient du score, le 1/2 de la probabilité qu'un joueur l'emporte je suppose ? Mais le reste ? Quelle formule est utilisée ici ?

Merci encore.

@De-Perga a dit dans Exercice de probabilités casse-tête :

@Noemi

@Black-Jack a dit dans Exercice de probabilités casse-tête :

Ta réponse (club nord) sous-entend que la proba de faire (pour un joueur) un score de 5-4 est la même que celle de faire un score de 6-3 ou un score de 7-2 ou ...

Cela ne me semble pas du tout acquis, pour moi, les différents scores ne sont pas équiprobables, loin s'en faut.

Il me semble par exemple que la proba pour un joueur du score 9-0 est P(9;0) = 1 - (1 - 1/2^9) = 0,001953...
Et ceci en "oubliant" la qualité du joueur, sinon c'est inextricable.

Cette proba (0,001953) semble être confirmée par une simulation (j'ai simulé 140 fois 5000 parties de 9 jeux) et la moyenne du score 9-0 trouvé est 0,00195

A titre indicatif, la simulation donne une proba de 0,16 pour le score 6-3 (et pareil pour le score 3-6).

En effet, ça me semble logique que la probabilité que le joueur l'emporte avec 9-0 soit moins ''probable'' que de l'emporter avec 5-4 par exemple sans prendre en compte le niveau des joueurs (et donc que les différents scores ne soient pas équiprobables).

Je dois donc calculer, tel que Black-Jack, la probabilité que chaque score se réalise pour ensuite pouvoir modifier mon calcul de probabilité réalisé précédemment pour avoir une approche plus juste de la réalité ?

Cependant, pour ce qui est de la probabilité P(9-0) = 1 - (1 - 1/2^9) = 0,00195 : le 9 provient du score, le 1/2 de la probabilité qu'un joueur l'emporte je suppose ? Mais le reste ? Quelle formule est utilisée ici ?

Merci encore.

Bonjour,

Ce que j'en pense ;

Autre manière de calculer.

Pour avoir x victoire sur 9 jeux, la proba est P(x) = C(9,x)/2^9
avec C(9,x) le combinaison de x jeux parmi 9

Pour gagner 9 matchs sur 9, la proba est donc P(9) = C(9,9)/2^9 = 1/2^9 = 1/512 (= 0,001953125)
Pour gagner 6 matchs sur 9, la proba est donc P(9) = C(9,6)/2^9 = 84/512 = 21/128 (= 0,1640625)

ceci pour les joueurs des clubs du Nord.

Pour les autres clubs, il faudrait y réfléchir.

Peut-être que je me trompe ... mais je ne pense pas que c'est le cas.

Quant à savoir ce qu'en pense le prof ...

@Black-Jack a dit dans Exercice de probabilités casse-tête :

@De-Perga a dit dans Exercice de probabilités casse-tête :

@Noemi

@Black-Jack a dit dans Exercice de probabilités casse-tête :

Ta réponse (club nord) sous-entend que la proba de faire (pour un joueur) un score de 5-4 est la même que celle de faire un score de 6-3 ou un score de 7-2 ou ...

Cela ne me semble pas du tout acquis, pour moi, les différents scores ne sont pas équiprobables, loin s'en faut.

Il me semble par exemple que la proba pour un joueur du score 9-0 est P(9;0) = 1 - (1 - 1/2^9) = 0,001953...
Et ceci en "oubliant" la qualité du joueur, sinon c'est inextricable.

Cette proba (0,001953) semble être confirmée par une simulation (j'ai simulé 140 fois 5000 parties de 9 jeux) et la moyenne du score 9-0 trouvé est 0,00195

A titre indicatif, la simulation donne une proba de 0,16 pour le score 6-3 (et pareil pour le score 3-6).

En effet, ça me semble logique que la probabilité que le joueur l'emporte avec 9-0 soit moins ''probable'' que de l'emporter avec 5-4 par exemple sans prendre en compte le niveau des joueurs (et donc que les différents scores ne soient pas équiprobables).

Je dois donc calculer, tel que Black-Jack, la probabilité que chaque score se réalise pour ensuite pouvoir modifier mon calcul de probabilité réalisé précédemment pour avoir une approche plus juste de la réalité ?

Cependant, pour ce qui est de la probabilité P(9-0) = 1 - (1 - 1/2^9) = 0,00195 : le 9 provient du score, le 1/2 de la probabilité qu'un joueur l'emporte je suppose ? Mais le reste ? Quelle formule est utilisée ici ?

Merci encore.

Bonjour,

Ce que j'en pense ;

Autre manière de calculer.

Pour avoir x victoire sur 9 jeux, la proba est P(x) = C(9,x)/2^9
avec C(9,x) le combinaison de x jeux parmi 9

Pour gagner 9 matchs sur 9, la proba est donc P(9) = C(9,9)/2^9 = 1/2^9 = 1/512 (= 0,001953125)
Pour gagner 6 matchs sur 9, la proba est donc P(9) = C(9,6)/2^9 = 84/512 = 21/128 (= 0,1640625)

ceci pour les joueurs des clubs du Nord.

Pour les autres clubs, il faudrait y réfléchir.

Peut-être que je me trompe ... mais je ne pense pas que c'est le cas.

Quant à savoir ce qu'en pense le prof ...

Correction :

Lire : Pour gagner 6 matchs sur 9, la proba est donc P(6) = C(9,6)/2^9 = 84/512 = 21/128 (= 0,1640625)

@Black-Jack

@Black-Jack a dit dans Exercice de probabilités casse-tête :

Pour avoir x victoire sur 9 jeux, la proba est P(x) = C(9,x)/2^9
avec C(9,x) le combinaison de x jeux parmi 9

Pour gagner 9 matchs sur 9, la proba est donc P(9) = C(9,9)/2^9 = 1/2^9 = 1/512 (= 0,001953125)
Pour gagner 6 matchs sur 9, la proba est donc P(6) = C(9,6)/2^9 = 84/512 = 21/128 (= 0,1640625)

Je ne suis pas très bon en maths, ça se voit car je n'arrive pas à comprendre le détail du ''C(9,9) ou C(9,6)''. D'où provient le 84 ?
Et si j'arrive à comprendre le détail de la formule, est-ce applicable au club du Sud ? Sachant que leur match s'arrête une fois le premier arrivé à 6.

Si je reprend mon calcul :

$P_D$ (N) = $P(D).P(N)P(D)\dfrac{P(D).P(N)}{P(D)}$ = $P(D).P(N)PN(D)+PS(D)\dfrac{P(D).P(N)}{P_N(D)+P_S(D)}$ = $0.2∗0.7(0.2∗0.7)+(1/6∗0.3)\dfrac{0.2 * 0.7}{(0.2*0.7)+(1/6 *0.3)}$ ≈ $0.737 = 74$ %

en remplaçant les valeurs par les vrais probabilités d'obtenir un score et donc sans admettre qu'elles soient équiprobables, je dois chercher la probabilité $P_S(D)$ et $P_N(D)$ . Si je me base sur le calcul que tu as effectué, j'aurais : $P_N(D)$ $=$ $(0.164 * 0.7)$ $=$ $0.1148$

(Sachant que D est égal à la probabilité d'obtenir le score de 6-3 pour un membre du club du Nord : correspondant bien à la probabilité de gagner 6 matchs sur 9 que tu as calculé).

Il ne me manquerait donc, une fois le détail du calcul compris, de trouver $P_S(D)$ afin de pouvoir calculer la probabilité de $P_D$ (N).

Ps : Merci de prendre du temps pour m'expliquer tout ceci.

Bonsoir,

Explication pour la probabilité pour les clubs du Nord.

Je le fais avec des valeurs plus petites pour faire comprendre (car on peut alors noter toutes les possibilités)

Supposons qu'on doive jouer 3 matchs et qu'on veut la proba d'en gagner 2

On note tous les séries de matchs possibles (0 pour perdu et 1 pour gagné)
000
001
010
011
100
101
110
111

Il y a donc 8 groupement possibles (qu'on trouve par 2^3, le 3 est le nombre de matchs joués par 1 joueur)

On note les combinaisons de matches qui donnent 2 victoires :
110
101
011

Il y en a 3 qu'on calcule par C(3,2)
Avec C(3,2) le nombre de combinaisons de 2 victoires sur 3 matches

La proba qu'un joueur gagne 2 matches sur 3 est donc : C(3,2)/2^3 = 3/8

Dans le cas de l'exercice, on a 9 matches, soit 2^9 = 512 séries de matchs possibles

Ceux avec 6 victoires se calcule par C(9,6)

La proba qu'un joueur gagne 3 matches sur 9 est donc : C(9,6)/2^9 = 84/512 (qu'on peut simplifier en 21/128)

Pour calculer la combinaison(n,m), on fait : C(n,m) = n!/(m! * (n-m)!)

n! pour factorielle n , n! = n * (n-1) * (n-2) * ... * 2 * 1

donc par exemple C(9,6) = 9!/(6! * (9-6)!) = 9!/(6! * 3!)
C(9,j6) = (98765432)/(65432 * 3 * 2) = (987)/(3 2) = 504/6 = 84

A supposé que c'est cela qui est attendu dans les calculs ... ce n'est valable que pour les clubs du Nord.

... il faut maintenant trouver le raisonnement pour les clubs du Sud. (ce que je n'ai pas essayé)

@De-Perga

As-tu compris le calcul avec les combinaisons ?
Si oui fais le calcul pour chaque cas de l'arbre.

@Noemi

C'est en effet très bien expliqué, j'essaie en ce moment de le faire pour la partie club sud.

Rebonjour,

Principe pour les clubs du sud

Décompte des possibilités:

gain par 6-0 : 1 seule possibilité (que je noterais 111111)

gain par 6-1 : plusieurs possibilités.
Mais on peut dire que le score avant le dernier match était de 5-1 (réfléchir pourquoi)
Les possibilités pour arriver à 5-1 sont au nombre de 6 sont :
011111
101111
110111
111011
111101
111110
Ce nombre est calculé par C(6,5) = 6
Le gain par le score de 6-1 est donc possible de 6 manières différentes.

gain par 6-2 : plusieurs possibilités.
Mais on peut dire que le score avant le dernier match était de 5-2 (réfléchir pourquoi)
Les possibilités pour arriver à 5-2 est calculé par C(7,5) = 21
Le gain par le score de 6-2 est donc possible de 21 manières différentes.

A toi pour calculer le nombres de chemins possibles pour gagner par 6-3 ; 6-4 ; 6-5

On recommence en calculant les chemins possibles pour perdre par 0-6 ; 1-6 ; 2-6 ; .... ; 5-6

Quand ce sera fait, tu additionnes tous les chemins possibles de gain ou de perte, soit N ce nombre

La proba de gagner par 6-3 est alors : (nombre de manières de gagner 6-3)/N

Arriver à ce stade, il y aura tout ce qu'il faut pour répondre à la question de l'énoncé.

Sauf étourderie de ma part.

@Black-Jack et @Noemi

Donc c'est bien à ce moment qu'il faut calculer le score qui précède le dernier avant la victoire ! Je savais bien qu'il fallait le faire à un moment..

J'ai donc bien résumé ce que j'ai compris dans un tableur.
On obtient donc pour les Clubs du Nord :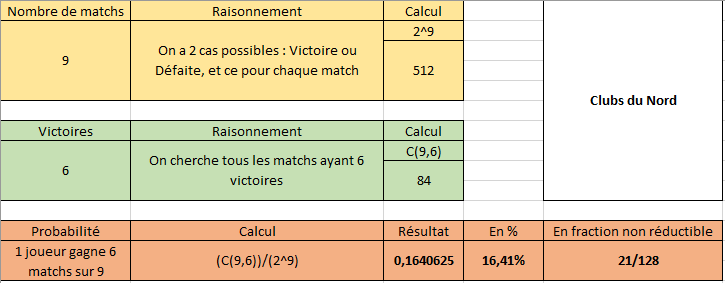

Et pour les Clubs du Sud :

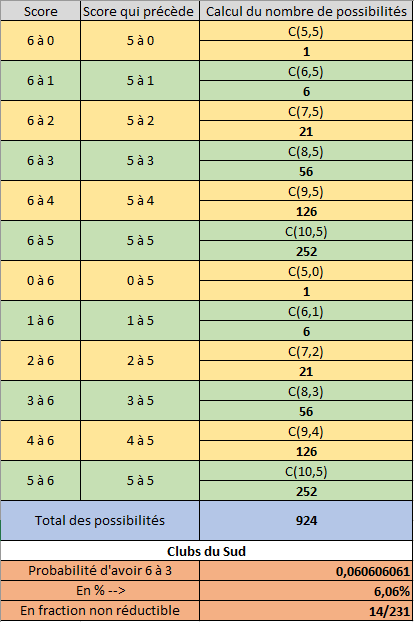
D correspond à un match gagné 6-3.
J'ai donc :

$P_N$ (D) =21/128 = 0,1640625 = 16,41%.
$P_S$ (D) =14/231 = 0,060606061 = 6,06%.

ainsi que les autres paramètres connus :

$P$ (N) = 0,3 = 30%
$P$ (S) = 0,7 = 70%

Et je veux calculer la probabilité qu'un joueur ayant gagné 6-3 soit un joueur du club du Nord : $P_D$ (N).

Je reprend donc mon calcul :

$P_D$ (N) = $P(D).P(N)P(D)\dfrac{P(D).P(N)}{P(D)}$ = $P(D).P(N)PN(D)+PS(D)\dfrac{P(D).P(N)}{P_N(D)+P_S(D)}$ = $0.3∗0.7((21/128)+(14/231))\dfrac{0.3 * 0.7}{((21/128)+(14/231))}$ ≈ $0, 9347 = 93$ %

Si j'ai bien compris je dois pas prendre en compte le % de clubs dans la probabilité $P$ (D) car celui-ci est compris dans nos calculs des possibilités d'obtenir un match 6-3 dans chacun des clubs (j'espère être compréhensible).

Cela me semble élevé, ais-je fait une erreur ?

@De-Perga
Une erreur dans le calcul de pourcentage pour les clubs du sud.
Il faut utiliser la valeur exacte soit 0,0606.... qui donne une fraction de 2/33.

Pour le calcul des différentes probabilités applique le même raisonnement que pour la première approche
$P(D∩N)=0,7×21/128=147/1280=0,1148P(D\cap N)=0,7\times 21/128 = 147/1280 = 0,1148$

@Noemi
Oui en effet (j'ai rentré à la main les fractions non réductibles). Et si l'on divise 14 par 7 et 231 par 7 on obtient bien 2/33. Je ne suis donc pas allé jusqu'au bout mais sinon la valeur reste la même ?

Je viens de voir que je me suis trompé dans la formule de Bayes (j'ai mis $P (D)$ . $P (N)$ au lieu $P_D$ (N). $P (N)$ :

$P_D$ (N) = $PN(D).P(D)P(N)\dfrac{P_N(D).P(D)}{P(N)}$ = $PN(D).P(D)P(N)\dfrac{P_N(D).P(D)}{P(N)}$ = $(21/128).(21/128+2/33)0,7\dfrac{(21/128).(21/128+2/33)}{0,7}$ = $0.0527$ = $5$ %

Trop faible maintenant..

Pour le calcul des différentes probabilités applique le même raisonnement que pour la première approche
$P(D∩N)=0,7×21/128=147/1280=0,1148P(D\cap N)=0,7\times 21/128 = 147/1280 = 0,1148$

La première approche ? A quel niveau du calcul ?

@De-Perga

Voir la formule que j'ai indiquée dans un des premiers post.
Vérifie l'écriture de ta formule. Tu dois calculer la probabilité que le gagnant vient du club du nord sachant qu'il a gagné avec le score 6-3.

@Noemi a dit dans Exercice de probabilités casse-tête :

@De-Perga

Utilise :
$P_D(N)$ = $P(D∩N)P(D)\dfrac{P{(D\cap N)}}{P(D)}$

C'est bien celle-ci ?

Si je la reprends :

$P_D(N)$ = $P(D∩N)P(D)\dfrac{P{(D\cap N)}}{P(D)}$ = $P(D)∗P(N)P(D)\dfrac{P{(D) * P(N)}}{P(D)}$ = $(PN(D)+PS(D))∗P(N)PN(D)+PS(D)\dfrac{(P_N{(D) + P_S(D))* P(N)}}{P_N(D) + P_S(D)}$ = $(21/128+2/33)∗0.721/128+2/33\dfrac{({21/128 + 2/33)* 0.7}}{21/128 + 2/33}$ = 0.7

Ce qui me semble normal vu que les deux groupes de valeurs s'annulent, il nous reste 70% soit la proportion des clubs du Nord. Un problème dans la formule ?

@De-Perga

Le calcul est à revoir.

Exercice de probabilités casse-tête

La proba qu'un joueur gagne 2 matches sur 3 est donc : C(3,2)/2^3 = 3/8

La proba qu'un joueur gagne 3 matches sur 9 est donc : C(9,6)/2^9 = 84/512 (qu'on peut simplifier en 21/128)

donc par exemple C(9,6) = 9!/(6! * (9-6)!) = 9!/(6! * 3!) C(9,j6) = (98765432)/(65432 * 3 * 2) = (98*7)/(3 * 2) = 504/6 = 84

donc par exemple C(9,6) = 9!/(6! * (9-6)!) = 9!/(6! * 3!)
C(9,j6) = (98765432)/(65432 * 3 * 2) = (987)/(3 2) = 504/6 = 84