Position relative de deux courbes

Bonjour/Bonsoir,
j'espère que vous passez un bon moment durant les vacances.

J'aimerais que vous m'aidez à resoudre l'exercice suivant SVP :
f et g sont deux fonctions définies sur R par :

f(x) = (x- l)3 et g(x) = X - 1.
On note Cf et Cg les courbes représentatives respectives des fonctions f et g.

a. À l’aide d'un logiciel de géométrie dynamique, construire dans un repère les courbes f et g.
b. Quelles conjectures peut-on faire au sujet de la position relative de ces deux courbes ?
c. h est la fonction définie sur R par :
h(x) = fix) - g(x).
Résoudre l'équation h(x) = 0.

En déduire les coordonnées des points communs aux courbes Cf et Cg.

d) Résoudre les inéquations h(x) ≤ 0 et h(x) ≥ 0.

En déduire la position relative des courbes Cf et Cg.
On pourra construire un tableau de signes pour h(x).
2) x est un nombre réel appartenant à l'intervalle [0 ; 1). On note M le point d’abscisse x de la courbe Cf et N le point d'abscisse x de la courbe Cg,
a. À l'aide du logiciel, placer les points M et N, puis conjecturer les variations de la distance MN en fonction de x.
b. Justifier que pour tout x de l'intervalle [0 ; 1], MN = h(x).
c. Étudier les variations de la fonction h sur l’intervalle
[0 ; 1),
d) Montrer que la fonction h admet un maximum, que l'on déterminera, sur l’intervalle [0 ; 1]. La conjecture établie à la question 2a est-elle confirmée ?

J'ai construit les deux courbes a l'aide de geogebra (1a) mais je n'arrive pas à resoudre les questions qui viennent après.

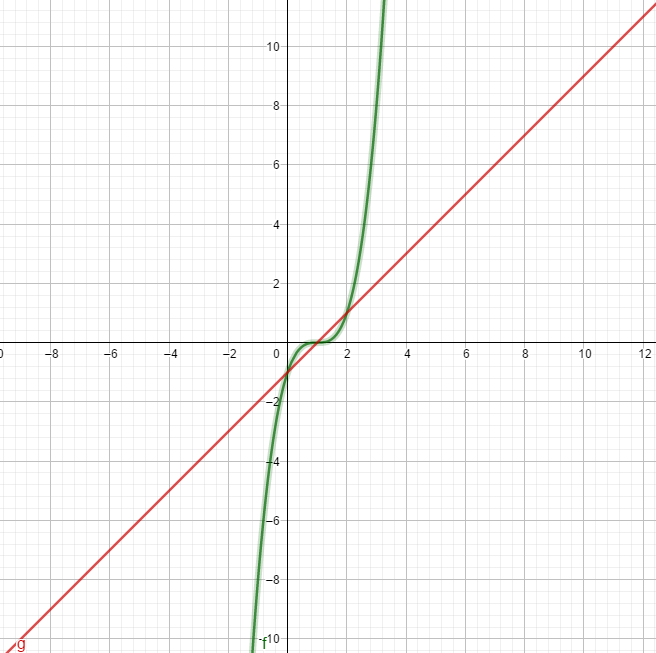
Screenshot 2020-12-26 211818.png

Bonsoir Prince-Of-Darkness,

Pour la position relative des deux courbes, indique selon les valeurs de $x$ , celle qui est au dessus de l'autre.
Pour $x<0x\lt0$ , $g$ est au dessus de $f$ .
...

@Noemi Bonjour,
Desole pour la reponse retardee.

Pour x < 0, f(x) < g(x) sur l'intervalle }-infinie; 0{

Est-ce que c'est la bonne reponse?

@Prince-Of-Darkness

Tu dois analyser la position des deux courbes pour $x$ variant de $−∞-\infty$ à $+∞+\infty$ .

@Noemi F(x) ≤ g(x) sur }- infinie ; +{ U {1;2}

F(x) ≥ g(x) sur {0;1} U {2;+ infinie}

@Prince-Of-Darkness

Il faut mettre des crochets pour les intervalles
$]−∞;0]U[1;2]]-\infty ; 0] U [1;2]$

@Noemi Je les trouve pas sur mon clavier

Est-ce que je peux passer a la prochaine question ou ma reponse est erronee?

@Prince-Of-Darkness

Sur le clavier, il faut taper les touches majuscules option et parenthèse.

Tu peux passer à la question suivante.

@Noemi Merci []

Je n'arrive pas a resoudre l'equation (x-1)^3 - (x-1) car on a jamais appris a resoudre ce genre d'equation. pourriez-vous m'aider svp.

Commence par factoriser l'expression :
$x-1)^3-(x-1) = (x-1)[(x-1)^2-1] = ....$

Factorise le terme entre crochets.

(x-1)(x-1)^2-(x-1)
== (x-1)(x-1)^3-x+1
== (x-1)(x^2-2x-1-x+1)
== (x-1)(x^2-3)

x=1 ou x^2-3x=0
x(x-3)=0
x=0 ou x=3

S {0;1;3}
Qu'en pensez-vous?

@Prince-Of-Darkness

Des erreurs
$x-1)^3-(x-1) = (x-1)[(x-1)^2-1] =$
$x-1)(x^2 -2x+1-1) = (x-1)(x^2-2x) = (x-1)x(x-2)$

Je te laisse résoudre l'équation.

@Noemi (x-1)x(x-2)=0
x=1 ou x=0 ou x=2

S{ 1;0;2}

@Prince-Of-Darkness

Oui, mais mets les solutions dans l'ordre croissants : $S={0;1;2}S=\lbrace0 ; 1 ; 2\rbrace$

@Noemi Pour trouver les coordonees des points communs je lis graphiquement ou il y a un cacul a effectuer?

Puis pour résoudre les inéquations h(x) ≤ 0 et h(x) ≥ 0 j'utilise le meme calcul que vous avez fait ((x−1)x(x−2)) ?

@Prince-Of-Darkness

Pour trouver les coordonnées des points, tu as les abscisses, les valeurs trouvées précédemment, tu calcules les ordonnées.

Il est demandé de résoudre les inéquations, donc tu ne peux pas utiliser le graphique. Il te permet néanmoins de vérifier le résultat.

@Noemi Y0=h(0)=(0-1)^3-(0-1)=0
Y1=h(1)=(1-1)^3-(1-1)=0
Y2=h(2)=(2-1)^3-(2-1)=0

Est-ce que ce calul pour trouver les ordonnees est correct?

@Prince-Of-Darkness

Pour le calcul de l'ordonnée, tu choisis soit la fonction $f$ , soit la fonction $g$ .
Pour $x = 0$ , $g (0) = 0 - 1 = - 1$ soit le point $A (0, - 1)$ .
Fais le calcul pour $x = 1$ et $x = 2$ .

@Noemi J'ai fait trouve que l'ordonnee des 3 points est 0:

J'ai fini l'exercice qui suit le c :

Pour l'exercice qui suit le d (2), j'ai ajoute les deux points (M et N) mais je ne comprend pas il faut faire quoi apres.

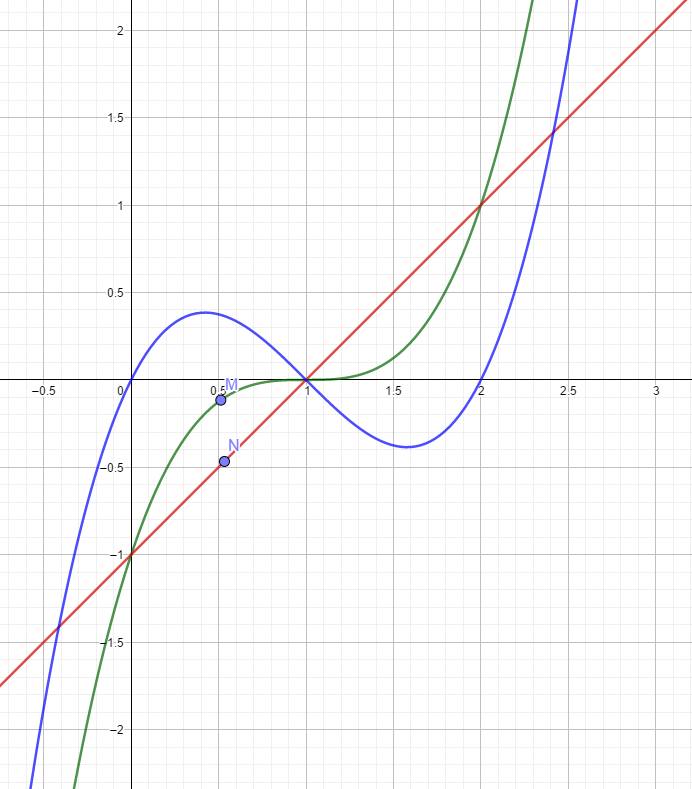
Screenshot 2020-12-28 214105.png

@Prince-Of-Darkness

Pour la question c), c'est correct. Tu aurais pu faire un tableau de signes comme indiqué dans l'énoncé. Tu aurais obtenu le résultat plus rapidement.

Pour la partie 2; trace le segment [MN] puis calcule la distance. Fais varier avec le logiciel la position des points pour pouvoir conjecturer comment varie la distance.

@Noemi J'observe que sur [0;0.45] la distance entre les deux points augment alors que sur l'intervalle ]0.45; 1] la distance diminue.

@Prince-Of-Darkness

Vérifie l'ordonnées des points.
Pas sur que ce soit 0,45 la borne mais la conjecture est correcte, la distance augmente puis diminue.

@Noemi Bonjour,

J'ai tout fait mais il me reste cette question :

Justifier que pour tout x de l'intervalle [0 ; 1], MN = h(x).

Je suis un peu bloque.

@Prince-Of-Darkness

Sur l'intervalle [0;1], la fonction $f$ est au dessus de la fonction $g$ ; la distance MN correspond donc à $f (x) - g (x)$ soit $h (x)$ .

@Noemi Monsieur/Madame, je vous remercie profondément pour votre gentillesse. Vous m'avez beaucoup aide. Bonne journee.

@Prince-Of-Darkness

Bonne journée, l'essentiel c'est que tu aies tout compris.