Dm de maths je comprend pas la première question
-
Uls_ zkh dernière édition par Uls_ zkh
Dans la figure ci dessus le tgl isocèle abc est isocèle en A , I est le milieu de BC , AI = 4cm, BC= 8cm A tout point M du segment AI on fait correspondre le rctgl EFGH tel que HG parallèle a BC et M appartient à HG. On pose AM = x
-
soit l’aire du rctgl EFGH en fonction de x. Donner l’ensemble de définition D de la fonction A
-
Montrer que pour tout x appartenant à D, A(x) = 2x(4-x)
Merci de m’expliquer.
-
-
@Uls_-zkh, Bonjour (Marque de politesse à ne pas oublier !!)
L'énoncé est-il complet ?
Les questions sont-elle dans le bon ordre ?
Comment est définie la fonction A ?
-
Uls_ zkh dernière édition par
@Noemi Bonjour désolé ^^ pour la fonction x rien est précisé à part que AM = x
-
-
Donc c'est la fonction AM=xAM = xAM=x ou comment varie xxx qui est demandé ?
Le point M se déplace sur le segment [AI][AI][AI], donc xxx varie de 0 à 4. -
Il faut remarquer que le triangle AIBAIBAIB est rectangle isocèle car III étant le milieu de BCBCBC, alors BI=4BI= 4BI=4 et comme AI=4AI=4AI=4. Cela donne AI=IBAI = IBAI=IB
De plus le triangle ABCABCABC étant isocèle en AAA, AIAIAI est donc la hauteur issue de AAA, Donc l'angle AIB=90°AIB= 90°AIB=90°.
Cherche les dimensions des côtés du rectangle.
-
-
Uls_ zkh dernière édition par
@Noemi ! Enfaite je ne peux pas savoir les dimensions du rectangle car ce n’est pas demandé et il n’y a pas les mesures pour le faire

-
Pour déterminer l'aire A(x)A(x)A(x) il te faut trouver les dimensions HGHGHG et HEHEHE en fonction de xxx.
L'aire étant HG×HEHG\times HEHG×HE
-
Uls_ zkh dernière édition par
@Noemi je n’ai pas les mesures de HG et de HE et on ne peut pas les trouver car les mesures donnés ne servent pas à trouver HG et he


 ️
️
-
Tu n'as pas analysé ce que j'ai noté.
Comme le triangle AIBAIBAIB est rectangle isocèle en I et que (HG)(HG)(HG) parallèle à (BC)(BC)(BC), en utilisant la propriété de Thalès dans les triangles AMHAMHAMH et AIBAIBAIB, tu déduis HM=xHM=xHM=x
Puis comme MI=AI−AM=4−xMI = AI-AM=4-xMI=AI−AM=4−x et HE=MIHE = MIHE=MI
L'aire du rectangle est donc 2x(4−x)2x(4-x)2x(4−x).
-
BBlack-Jack dernière édition par
Bonjour,
Par Thales ou par les triangles de même forme ...
AM/HM = AI/BI
x/HM = 4/4
--> HM = x
HG = 2.HM = 2xHE = MI = AI - AM
HE = 4 - x...
-
Uls_ zkh dernière édition par
@Noemi comment avez vous fait pour trouver quatre 4 ?
-
Le triangle AIBAIBAIB est rectangle isocèle en III, donc AI=BI=BC2=4AI = BI = \dfrac{BC}{2}= 4AI=BI=2BC=4.
-
mtschoon dernière édition par mtschoon

Bonjour,
Graphique.
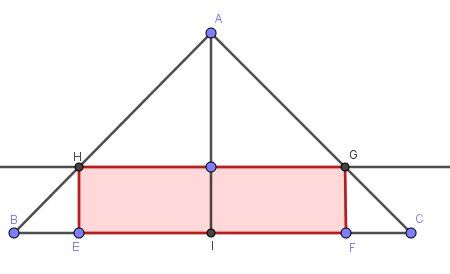
-
mtschoon dernière édition par

Bonjour,
La suite de l'exercice est ici :
https://forum.mathforu.com/topic/31542/factorisation-et-résolution-équation-du-second-degréComme déjà indiqué, il ne faut pas changer de topic au cours du même exercice...