Exercice Suites géométriques

Bonjour, j'ai un exercice sur les suites géométriques. Je suis bloquée à partir de la question 2 pouvez m'aider ?
Première question j'ai trouvé r=8

Merci d'avance

Lien supprimé par la modération.

Bonjour Chloé-Badet,

Le scan ou un lien de l'énoncé du sujet est interdit sur ce forum. Seuls les schémas, figures et graphiques sont autorisés.

Recopie l'énoncé et propose tes éléments de réponse.
Si r = 8. Quelle est donc la raison de la suite ?

Le lien va être supprimé.

@Chloé-Badet

Voici l'énoncé.

Une entreprise fabrique des flacons à l'aide de petits cubes.

L'arête du premier cube est 10cm
L'arête d'un cube autre que le premier est égal à la moitié de celle du cube précédent.
Pour tout n de N*, sur U n le volume du n-ième cube (à partir du bas).

Recopier et compléter: Lorsque les longueurs sont divisés par 2, les volumes sont divisés par ...: u est une suite géométrique de raison r -....
Calculer le volume total du flacon représenté ci-dessus ( constitué de 6 cubes). Arrondir au millième de mm3 (6 chiffres après la virgule).
Calculez le volume d'un flacon composé de n cubes. Simplifiez la formule autant que possible.
De quelle valeur se rapproche le volume du flacon lorsque l'on poursuit indéfiniment la construction. Donner la réponse sous forme de fraction irréductible,

@Chloé-Badet

Indique la raison puis calcule le volume total.

Bonjour,

Vu que ce topic ne semble pas abouti, j'indique quelques éléments pour consultation.

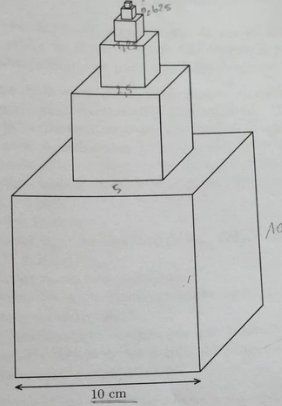
Les longueurs sont exprimées en $c m$ . Les volumes sont exprimés en $cm^3$

Lorsque les longueurs sont divisées par $2$ , les volumes sont divisés par $2^3=8$ , c'est à dire multipliés par $18\dfrac{1}{8}$

$U_n)$ est donc la suite géométrique de raison $q=18q=\dfrac{1}{8}$ et de premier terme $U_1=10^3$
(je note $q$ la raison car de façon traditionnelle la notation r est réservée aux suites arithmétiques)

Pour tout $n≥1n\ge 1$ ,
$Un=U1×qn−1=103×(18)n−1U_n=U_1\times q^{n-1}=10^3\times \biggl(\dfrac{1}{8}\biggl)^{n-1}$

$S_6=U_1+U_2+...+U_6$

En utilisant la formule de la somme :
$S6=U1×1−q61−qS_6=U_1\times \dfrac{1-q^6}{1-q}$

$S6=103×1−(18)61−18S_6=10^3\times \dfrac{1-\biggl(\dfrac{1}{8}\biggl)^6}{1-\dfrac{1}{8}}$
(à calculer au mieux)

De façon générale
$Sn=103×1−(18)n1−18S_n=10^3\times \dfrac{1-\biggl(\dfrac{1}{8}\biggl)^n}{1-\dfrac{1}{8}}$
(à transformer au mieux)

$lim⁡n→+∞(18)n=0\displaystyle \lim_{n\to +\infty}\biggl(\dfrac{1}{8}\biggl)^n=0$

Donc

$lim⁡n→+∞Sn=10378=80007\displaystyle \lim_{n\to +\infty}S_n=\dfrac{10^3}{\dfrac{7}{8}}=\dfrac{8000}{7}$

Bonne lecture.