Variations de suites
-
YYuri123453 dernière édition par Yuri123453
Bonsoir, pouvez vous m’aider pour les questions 3 et 4.
Voilà ce que j’ai fait :
3) U1=6
U2=4
U3=3
U4=2,5
La suite (Un) semble croissante.
4)a) U1=-1
U2=1/2
U3=5/4
U5=29/16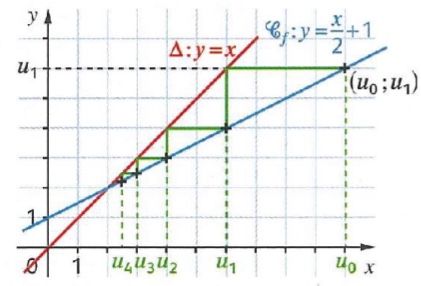
-
@Yuri123453 Bonsoir,
Le scan de l'énoncé du sujet est interdit sur ce forum. Seuls les schémas, graphiques ou figures sont autorisés.
Ecris l'énoncé et les questions si tu souhaites obtenir des éléments d'aide.
Pour la question 3, il s'agit de conjecturer le sens de variation de la suite en utilisant la construction.
Le scan va être effacé.
-
YYuri123453 dernière édition par
@Noemi
Voici donc les questions qui me bloque :
3) Conjecturer le sens de variation de la suite et sa limite éventuelles.
4)b) Conjecturer le sens de variation de la suite et sa limite éventuelles lorsque U0=-4
J’avais déjà fait la question 3 mais pour la 4b je bloque.
-
Il faut indiquer l'énoncé dans sa totalité.
Rectifie le résultat pour la question 3 et précise sa limite.Il manque l'énoncé de la question 4 a) et les éléments de réponse.
-
YYuri123453 dernière édition par Noemi
@Noemi
Voici l’énoncé dans son intégral :Soit (Un), la suite définie pour tout n E N par :
U0=10
Un+1= 1/2un + 1
On considère la fonction associé f définie sur R par :
f(x)= 1/2x + 1-
Dans un repère, construire la representation graphique Cf et la droite delta d’équation y=x.
2)a) Placer U0 sur l’axe des abscisses, puis construire U1=f(U0) sur l’axe des ordonnées.
b) A l’aide de la droite delta, ramener U1 sur l’axe des abscisses.
c) Réitérer ce procédé afin de construire U2,U3 et U4.
Voici la réponse de tout ça:
(Cf la photo du premier post) -
Conjecturer le sens de variation de la suite et sa limite éventuelle.
Réponse: U1= 1/2 x 10 + 1 = 6
U2= 1/2 x 6 + 1 = 4
U3= 1/2 x 4 + 1 = 3
U4= 1/2 x 3 + 1 = 2,5
La suite semble décroissante.
Lim n —-> - ♾
Un = - ♾
4)a) Construire les cinq premiers termes de la suite lorsque U0=-4
Réponse:
U1= -1
U2= 1/2
U3 = 5/4
U4= 13/8
U5= 29/16b) Conjecturer le sens de variation de la suite et sa limite éventuelle lorsque U0=-4.
La je bloque
-
-
Tu dois conjecturer à partir du graphique.
La suite est décroissante et sa limite semble être 2Pour la question 4 a) il faut faire le graphique et non les calculs et conjecturer le sens de variation et la limite éventuelle.
-
mtschoon dernière édition par mtschoon

Bonjour,
Quelques réflexions,
@Yuri123453 , si tu as besoin d'explications sur la construction des termes d'une suite , tu as un cours ici :
https://www.mathforu.com/premiere-s/representer-graphiquement-les-termes-d-une-suite/Pour ton énoncé de la 4)b), tu as dû faire une faute de frappe car il s'agit certainement de U0=−4U_0=-4U0=−4
Comme te le dit Noemi, dans ton exercice, tout n'est que graphique.
Remarque , si tu as la curiosité de chercher par le calcul la valeur de la limite LLL de la suite (convergente) :
LLL est l'abscisse (et l'ordonnée) du point d'intersection de la droite d'équation y=xy=xy=x avec la courbe d'équation y=f(x)y=f(x)y=f(x), donc LLL vérifie L=f(LL=f(LL=f(L) c'est à dire ici :
L=12L+1L=\dfrac{1}{2}L+1L=21L+1
En résolvant cette équation , tu auras la valeur de LLL.
-
mtschoon dernière édition par mtschoon

Si tu veux un graphique pour la 4)a)b) pour vérification, il faudra le demander.
-
YYuri123453 dernière édition par
@mtschoon
D’accord merci à vous deux
-
Le graphique :
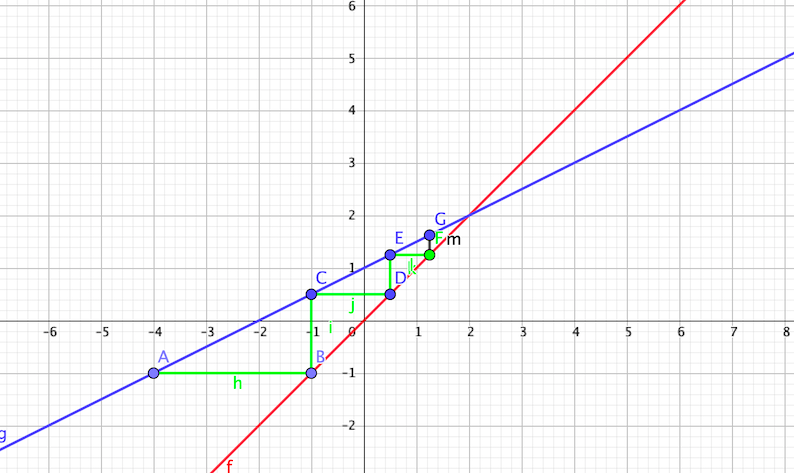
-
mtschoon dernière édition par mtschoon

De rien @Yuri123453 , bon travail.
Toutes ces conjectures "graphiques" seront ultérieurement démontrées mathématiquement (dans la suite de ton cours).