Déterminer les limites de fonction
-
Sofiane dernière édition par
Bonjour qui pourrait m'aider je suis perdu
Déterminer les limites des fonctions suivantes indiquéf(x)=e^2x-e^x +1 en + l'infini et - l'infini
f(x)=1/x(e^2x-1) en 0 et + Infini
f(x)=x+2+xe^x en - l'infini
-
@Sofiane Bonjour,
Pour la première fonction, mets exe^xex en facteur.
-
Sofiane dernière édition par
f(x)=e^2x-e^x +1
lim e^x
x tend vers + Infini
Bonjour vous voulez dire comme ceci
-
Non
f(x)=ex(ex−1+1ex)f(x) = e^x(e^x-1+\dfrac{1}{e^x})f(x)=ex(ex−1+ex1)
Cherche la limite de chaque terme lorsque xxx tend vers +∞+\infty+∞.
-
Sofiane dernière édition par
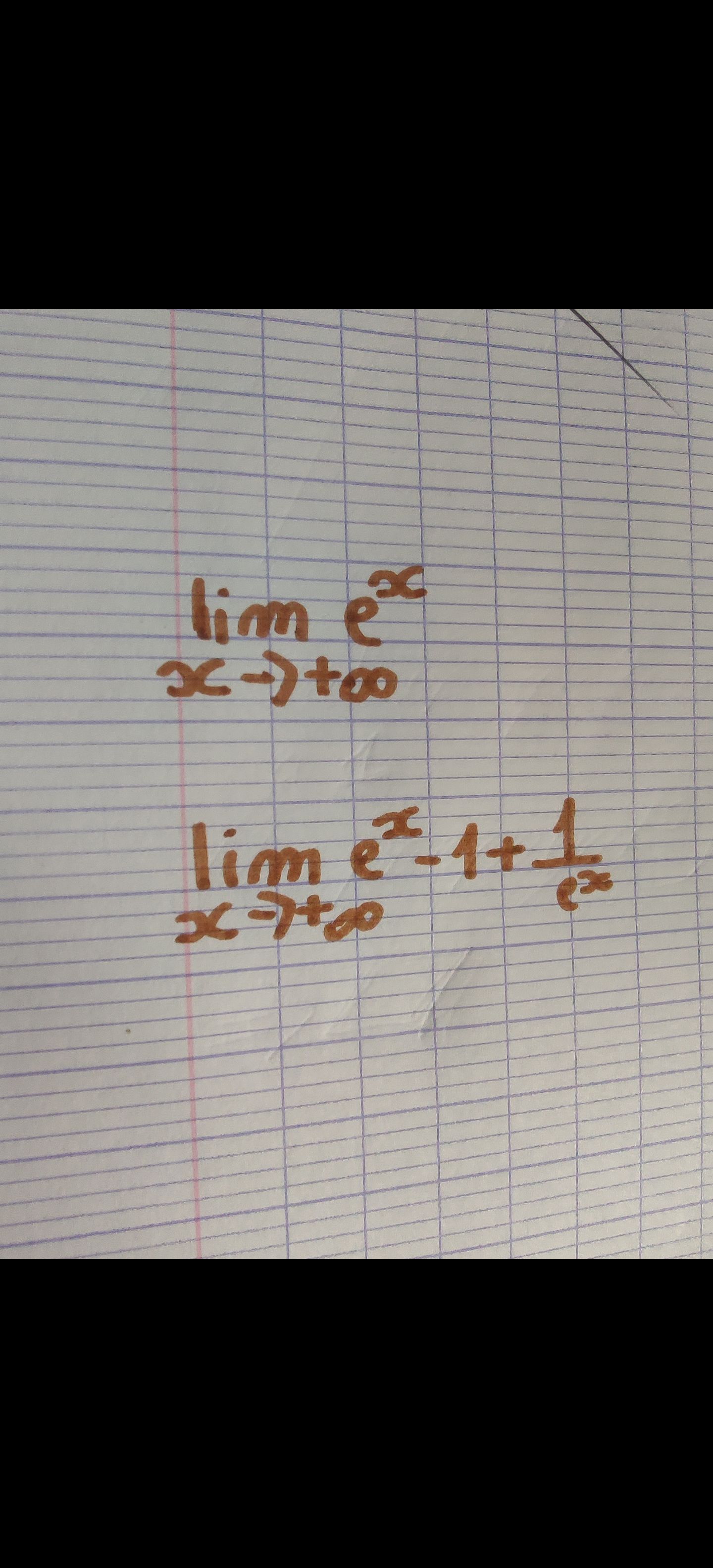
Comme ça
-
Oui, et quelle est la réponse pour chacune des limites ?
-
Sofiane dernière édition par
Comment on est censé la trouvé ?
-
Avec les limites de référence (voir le cours) que tu dois connaitre.
limx→+∞ex=+∞\displaystyle\lim_{x\to+\infty}e^x=+\inftyx→+∞limex=+∞
limx→−∞ex=0+\displaystyle\lim_{x\to-\infty}e^x=0^+x→−∞limex=0+
....
-
Sofiane dernière édition par
Ok je vais voir ça
-
Tu es en quelle classe ? Car tu postes en seconde ?
-
Sofiane dernière édition par
Ah j'ai du me tromper je suis en terminale
-
Sofiane dernière édition par
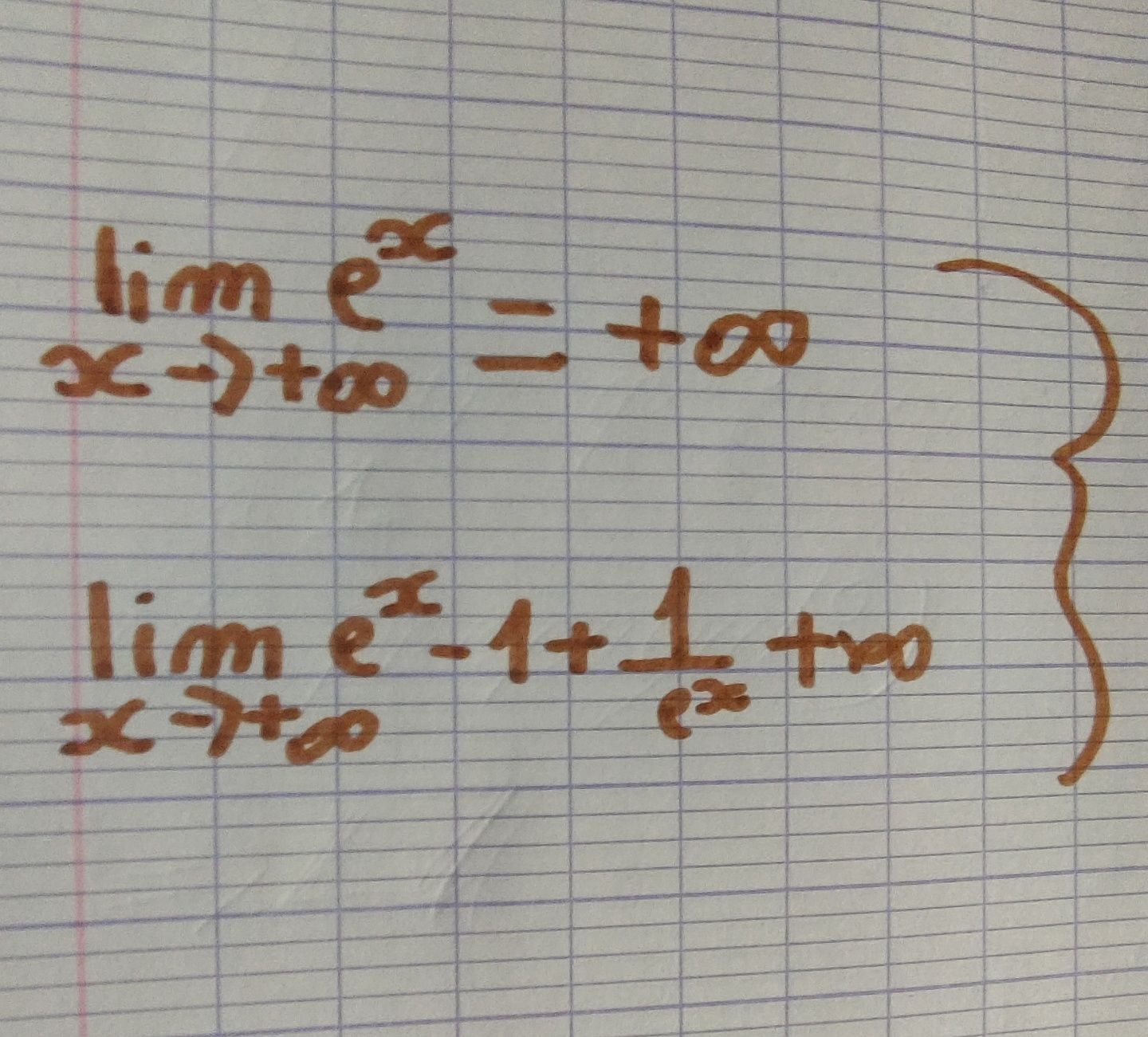 ensuite sa fait + l'infini c'est bien ça
ensuite sa fait + l'infini c'est bien ça
-
Oui donc la limite de la fonction est +∞+\infty+∞.
-
Sofiane dernière édition par
Juste pour la 3 comment on est censé faire il faut changé quelques choses car il y a une fraction ou non
-
Tu dois appliquer :
limx→−∞xex=0\displaystyle\lim_{x\to-\infty}xe^x=0x→−∞limxex=0
-
Sofiane dernière édition par
Ah ok merci
-
Sofiane dernière édition par
C'est bien cela ?
-
Propose tes réponses si tu souhaites une vérification.
-
Sofiane dernière édition par

-
Sofiane dernière édition par
Excusez moi il y'a eu un bug
-
Pour la première limite
en +∞+\infty+∞, ce n'est pas la somme des limites mais le produit.
en −∞-\infty−∞, tu calcules directement la limite sachant que :
limx→−∞ex=0+\displaystyle\lim_{x\to-\infty}e^x=0^+x→−∞limex=0+
Tu déduis que la limite est 1.Vérifie les limites pour les deux autres fonctions.
limx→0ex−1x=1\displaystyle\lim_{x\to0}\dfrac{e^x-1}{x}=1x→0limxex−1=1limx→+∞exx=+∞\displaystyle\lim_{x\to+\infty}\dfrac{e^x}{x}=+\inftyx→+∞limxex=+∞
-
Sofiane dernière édition par
Comme ceci sinon le reste c'est bon

-
Des erreurs
La première :
f(x)=e2x−ex+1f(x) = e^{2x}-e^x+1f(x)=e2x−ex+1
si xxx tend vers −∞-\infty−∞
Comme :
limx→−∞ex=0+\displaystyle\lim_{x\to-\infty}e^x=0^+x→−∞limex=0+
cela donne 0+0+1 soit comme limite 1La deuxième
f(x)=e2x−1xf(x)= \dfrac{e^{2x}-1}{x}f(x)=xe2x−1 Vérifie que c'est la bonne expression.
En 0, en utilisant :
limx→0ex−1x=1\displaystyle\lim_{x\to0}\dfrac{e^x-1}{x}=1x→0limxex−1=1limx→+∞exx=+∞\displaystyle\lim_{x\to+\infty}\dfrac{e^x}{x}=+\inftyx→+∞limxex=+∞
et en posant X=2xX=2xX=2x on trouve comme limite 2En +∞+\infty+∞
en utilisant
limx→+∞exx=+∞\displaystyle\lim_{x\to+\infty}\dfrac{e^x}{x}=+\inftyx→+∞limxex=+∞
On trouve comme limite +∞+\infty+∞Pour la troisième
la limite de x+2x+2x+2 en −∞-\infty−∞ est −∞-\infty−∞
donc la limite de f(x)f(x)f(x) est −∞-\infty−∞.Vérifie ces résultats et pose des questions si tu ne comprends pas.
-
Sofiane dernière édition par
Ok je vais voir ça
-
Sofiane dernière édition par
Je n'ai pas compris la 1 ère et pour la 2eme pourquoi avoir divisé par x ou c'est une erreur d'expression
-
Soit plus précis sur ce que tu n'as pas compris.
Pour la deuxième fonction, tu as écris : f(x)= 1/x(e^2x-1)La fonction est-elle ? f(x)=e2x−1xf(x)= \dfrac{e^{2x}-1}{x}f(x)=xe2x−1 ?
-
Sofiane dernière édition par
Cette partie je n'ai pas trop compris
Pourquoi 2: 0, 0cela donne 0+0+1 soit comme limite 1
Et pour la 2eme comment on fait pour simplifier car l'expression a changé ?
-
La première :
f(x)=e2x−ex+1f(x) = e^{2x}-e^x+1f(x)=e2x−ex+1
si xxx tend vers −∞-\infty−∞
Comme :
limx→−∞ex=0+\displaystyle\lim_{x\to-\infty}e^x=0^+x→−∞limex=0+
limx→−∞e2x=0+\displaystyle\lim_{x\to-\infty}e^{2x}=0^+x→−∞lime2x=0+
cela donne 0-0+1 soit comme limite 1La deuxième
f(x)=e2x−1xf(x)= \dfrac{e^{2x}-1}{x}f(x)=xe2x−1 Vérifie que c'est la bonne expression.
En 0, en utilisant :
limx→0ex−1x=1\displaystyle\lim_{x\to0}\dfrac{e^x-1}{x}=1x→0limxex−1=1
eX−1X2=2(eX−1X)\dfrac{e^{X}-1}{\dfrac{X}{2}}=2(\dfrac{e^{X}-1}{X})2XeX−1=2(XeX−1)en utilisant :
limx→0ex−1x=1\displaystyle\lim_{x\to0}\dfrac{e^x-1}{x}=1x→0limxex−1=1
On trouve comme limite en 0 la valeur 2Pour la limite en +∞+\infty+∞
En utilisant limx→+∞exx=+∞\displaystyle\lim_{x\to+\infty}\dfrac{e^x}{x}=+\inftyx→+∞limxex=+∞
On trouve comme limite +∞+\infty+∞
-
Sofiane dernière édition par
Ok merci je pense avoir compris donc normalement la tout est bon

-
La justification de la limite égale à 1 lorsque xxx tend vers −∞-\infty−∞ est à revoir.
La limite pour la troisième fonction est juste.
-
Sofiane dernière édition par
Ah oui sa reste plutôt - l'infini et non 1 si il y'a d'autres choses n'hésitez pas à me le souligner merci bien