Établir une formule pour cotan (2a) dans laquelle apparaîtra tan (a).

Bonjour, Pouvez-vous m'aider à résoudre cet exercice sur les formules d'addition et de duplication en trigo svp?
Voici l'énoncé : Établir une formule pour cotan (2a) dans laquelle apparaîtra tan (a).

@Joyca-Le-Boss Bonjour,

Commence par écrire les relations que tu peux appliquer.

@Noemi je connais la formule de tan(2a) mais pas celle de cotan(2a) !
On peut dire que cotan(2a) = 1/tan(2a) donc inversé la formule !!! Est-ce correct ?

@Noemi Voici la formule :
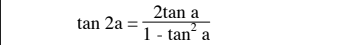
2021-02-06 (6).png

@Joyca-Le-Boss

Donc $c o t a n (2 a) = . . .$

@Noemi je ne suis pas sur mais peut-être l'inverse de la formule de tan(2a) donc cotan(2a): 1-tan2 a/ 2tan a
Est-ce correct comme raisonnement vu que cotan égale a l'inverse de la tangente ?

@Noemi C bon,j'ai trouver les formules
2021-02-07 (2).png

@Joyca-Le-Boss

Tu dois écrire en fonction de $t a n (a)$ , donc utilise :
$\dfrac{1}{tan(a)}$

@Noemi Et ensuite,on, doit l'injecter dans la formule de cotan(2a) ?

@Joyca-Le-Boss

Non utilise la relation de $t a n (2 a)$ .

@Noemi J'ai une idéé on peut dire que cotan(2a) = cotan(a+a) = est applique la formule d'addition ?

@Noemi En utilisant la relation tan(2a) =1/ 2tana / 1-tan2 a
J'ai utiliser l'inverse de la formule de tan(2a) car cotan(2a) = 1/ tan(2a)
Mon raisonnement est il correct ?

@Joyca-Le-Boss

Il manque un 1/ dans ta relation.
$\dfrac{1-tan^2(a)}{2tan(a)}$

@Noemi AH OUI !!! ENSUITE QUE FAIT - ON SVP?

@Joyca-Le-Boss

C'est terminé.

@Noemi Ok merci INFINIMENT !!!!!