Calculer cos(2a) si tg(a)=2 et préciser le quadrant auquel appartient 2a.

Bonjour, Pouvez-vous m'aider a résoudre cet exercices sur les formules d'addition et de duplication en trigo svp?
Voici l'énoncé : Calculer cos(2a) si tg(a)=2 et préciser avec exactitude le quadrant auquel appartient 2a.

@Joyca-Le-Boss Bonjour,

Indique tes calculs.

@Noemi Je dirais qu'il faudrait utiliser la formule en fonction de l'angle demie (a/2)
Cet formule ci :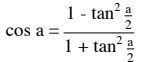 2021-02-06 (11).png

@Joyca-Le-Boss

Applique cette relation.

@Noemi On a la tg(a)=2,on veut trouver cos(2a)= cos2 a -sin2 a
Ensuite on trouve cos(a) avec cet formule =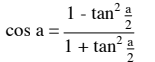 2021-02-06 (11).png
et ensuite on met le met au carré le cos(a) et puis il nous reste plus qu'a trouvé sin2 a
Est-ce correct comme raisonnement ?

@Joyca-Le-Boss

Avec la formule tu as directement cos(2a).

@Noemi Avec quel formule ?
Celle-ci :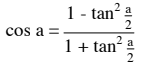 2021-02-06 (11).png
Ensuite on remplace tan2 (a/2) par (1/2) au carré, Est-ce correct?

@Joyca-Le-Boss

avec cette formule tu peux écrire :
$\dfrac{1-tan^2(a)}{1+tan^2(a)}$

@Noemi et ensuite on remplace tan2(a) par 4 vu que tg(a) = 2 et si on le met a carré ca vaut 4
Est-ce correct ?

@Joyca-Le-Boss

Oui fais le calcul.

@Noemi J'ai trouver Cos(2a)=-3/5 Donc c'est soit le Quadrant 2 ou soit le 4 mais pour le savoir avec exactitude ,il faut trouver le sin(2a). Est-ce correct?

@Joyca-Le-Boss

Oui calcule sin(2a).

@Noemi J'ai trouver que sin(2a)=4/5 donc 2a est dans le quadrant 2 vu que le cos(2a) =-3/5
Est-ce correct?

@Joyca-Le-Boss

C'est juste.

@Noemi OK merci énormément !!!!