Déterminer cos(a+b) et sin(a+b) à partir de cos(a) et tan(b).

[Joyca Le Boss]

Bonjour, Pouvez-vous m'aider a résoudre cet exercices sur les formules d'addition et de duplication en trigo svp?
Voici l'énoncé : Si cosa=1/4 où a∈ [0,π/2] et tg b=4 où b∈[π,3π/2] détermine cos(a+b) et sin(a+b).

[Noemi]

@Joyca-Le-Boss Re-Bonjour,

Cherche la relation à utiliser.
Une piste
A partir de $cos(a)=\frac{1}{4}$ déduis $sin(a)$ sachant que $a$ appartient ai cadran 1.
A partir de $tan(b)=4$, cherche $cos(2b)$ puis $sin(b)$ et $cosb$ sachant que $b$ appartient au cadran 3.

[Joyca Le Boss]

@Noemi J'ai trouver que le sin(a) = la racine de 15/4 ,j'ai utiliser cet formule :
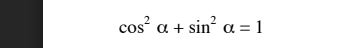
Est-ce correct ?

[Noemi]

@Joyca-Le-Boss

C'est juste.

[Joyca Le Boss]

@Noemi J'ai trouver que cos(2b) = -15/17 Est-ce correct ?

[Noemi]

@Joyca-Le-Boss

C'est juste.

[Joyca Le Boss]

@Noemi Mais a partir de là ,comment fait-on pour trouver sin(b) et cos(b) svp ?
De plus ,nous avons deja cos(b) qui vaut 1/4 et sin(b) qui vaut - la racine de 15/17

[Noemi]

@Joyca-Le-Boss

C'est $cos(2b)=-\frac{15}{17}$
Tu appliques $cos(2b)=1-2si{n}^2(b)$ et $cos(2b)=2co{s}^2(b)-1$
pour déterminer $sin(b)$ et $cos(b)$.

[Joyca Le Boss]

Ce message a été supprimé !

[Joyca Le Boss]

@Noemi j'ai pas compris pourquoi cos(2b)=1−sin 2 (b),Pouvez-vous me l'expliquer svp ?

[Noemi]

@Joyca-Le-Boss

C'est une relation que tu dois avoir dans le cours.
avec
$cos(2b)=co{s}^2(b)-si{n}^2(b)$

[Joyca Le Boss]

@Noemi Mais j'ai pas compris d'ou sort le 1 svp ?

[Noemi]

@Joyca-Le-Boss

A partir de $co{s}^{2}b+si{n}^{2}b=1$ tu peux déduire les deux relations que j'ai indiquées pour $cos(2b)$

[Joyca Le Boss]

@Noemi J'ai trouver que sin(b)=8racine de 17 /17
Est-ce correct ? Pouvez-vous me le confirmer svp ?

[Noemi]

@Joyca-Le-Boss

Vérifie tes calculs, tu dois trouver :
$sin(b)=-\frac{4\sqrt{17}}{17}$

[Joyca Le Boss]

@Noemi OUI je viens de me corriger ,j'ai également trouver 4racine de 17/17 !!!!

[Noemi]

@Joyca-Le-Boss

calcule $cos(b)$.

[Joyca Le Boss]

@Noemi J'ai trouve cos(b)= la racine de 1 /17
Est-ce correct ?Pouvez-vous me le confirmer ?

[Noemi]

@Joyca-Le-Boss

L'angle est dans le troisième cadran, donc son cosinus est négatif
$cos(b)=-\frac{\sqrt{17}}{17}$

[Joyca Le Boss]

@Noemi Ah oui, c'était le truc à ne pas oublier !!!!
Comment avez-vous trouver racine de 17/17 ?
Pouvez-vous me l'expliquer svp?

[Noemi]

@Joyca-Le-Boss

Il te reste à calculer :
$cos(a+b)$ et $sin(a+b)$

[Joyca Le Boss]

@Noemi Moi j'ai pas trouver racine de 17 /17
j'ai trouver racine de 1 /17
Pouvez-vous m'expliquer votre raisonnement svp ?

[Noemi]

@Joyca-Le-Boss

$\sqrt{\frac{1}{17}}=\frac{\sqrt{17}}{17}$

[Joyca Le Boss]

@Noemi ah donc vous avez juste rationnaliser !!!!

[Joyca Le Boss]

@Noemi Donc,en resumé ,nous avons Cos(b)=-racine de17 /17
Sin(b)= 4 racine de 17 /17
Sin(a) = racine de 15 /4
Cos(a)= 1/4
Est-ce correct?

[Noemi]

@Joyca-Le-Boss

Il manque le signe moins pour $sin(b)$ car $b$ est dans le cadran 3.

[Joyca Le Boss]

@Noemi ah oui exactement !!!

[Joyca Le Boss]

@Noemi Je peux faire le calcul a la calculatrice ou sans? ,mon prof n'a rien indiqué dans la consigne.

[Noemi]

@Joyca-Le-Boss

A mon avis c'est la valeur exacte qui est demandé, donc fais le calcul sans la calculatrice.
Tu appliques les relations :
$cos(a+b)=....$
$sin(a+b)=....$

[Joyca Le Boss]

@Noemi J'ai trouver pour cos(a+b)=- le racine de 255 - 4 fois la racine de 17 le tout sur 68
Est-ce correct ?

[Noemi]

@Joyca-Le-Boss

Je trouve :
$cos(a+b)=(\sqrt{15}-\frac{1}{4})\frac{\sqrt{17}}{17}$

[Joyca Le Boss]

@Noemi Pourquoi n'avez-vous pas mis le -4 devant le le racine de 17 /17
pouvez-vous m'expliquer svp ?

[Joyca Le Boss]

@Noemi Pour le sin(a+b) j'ai trouver pareil que le cos(a+b)
Est-ce correct ?

[Noemi]

@Joyca-Le-Boss

J'ai factorisé.
$cos(a+b)=-\frac{1}{4}\times \frac{\sqrt{17}}{17}+\frac{\sqrt{15}}{4}\times$ $4\frac{\sqrt{17}}{17}$

[Joyca Le Boss]

@Noemi AH nn c bon j'ai compris !!!

[Noemi]

@Joyca-Le-Boss

Le $cosa$ est positif mais le $cosb$ est négatif, donc le produit est négatif.

Le $sin(a+b)$ est différent de $cos(a+b)$.

[Joyca Le Boss]

@Noemi Pour le sinus j'ai trouver pareille que le cos(a+b)
Est-ce normal?
Qu'avait vous trouver pour le sin(a+b) = ? svp

[Joyca Le Boss]

@Noemi Je rectifie pour le sin(a+b) j'ai trouver pareille que le cos(a+b) mais avec le signe positif car les signes s'annulent !
Est-ce correct ? Pouvez-vous me le confirmer svp ?

[Noemi]

@Joyca-Le-Boss

$cos(a+b)=-\frac{1}{4}\times \frac{\sqrt{17}}{17}+\frac{\sqrt{15}}{4}\times$ $4\frac{\sqrt{17}}{17}$

$cos(a+b)=\frac{\sqrt{17}}{17}(-\frac{1}{4}+\sqrt{15})$

$sin(a+b)=-\frac{\sqrt{15}}{4}\times \frac{\sqrt{17}}{17}-4\frac{\sqrt{17}}{17}\times \frac{1}{4}$

$sin(a+b)=-\frac{\sqrt{17}}{17}(\frac{\sqrt{15}}{4}+1)$

[Joyca Le Boss]

@Noemi Merci Infiniment !!!!