Suite géométrique, recherche de 5 nombres.

[Joyca Le Boss]

Bonjour, Pouvez-vous m'aider à résoudre cet exercice, je les commencer mais je ne sais pas quoi faire après pouvez-vous me mettre sur la voie svp ?
Cinq nombres forment une suite géométrique, quels sont ces nombres si la somme des trois premiers vaut 30 et celle des trois derniers vaut 120 ?
Voici l'exercice que j'ai commencé :

Je pense qu'il faut que je trouve U1 !

[Noemi]

@Joyca-Le-Boss Bonjour,

Au départ 5 nombres, donc les relations sont :
$u_1+u_2+u_3=30$ et
$u_3+u_4+u_5=120$
Vu que $u_3$ est commun aux deus relations, écris chaque terme en fonction de $u_3$.
Tu obtiens ensuite une relation ne dépendant que de la raison de la suite.
Tu résous cette équation.

[Joyca Le Boss]

@Noemi mais on a aucune indication pour la raison ? comment dois-je faire pour le trouver svp ?

[Noemi]

@Joyca-Le-Boss

C'est une suite géométrique :
$u_3=u_2\times q$, soit $u_2=\frac{u_3}{q}$

$u_2=u_1\times q$, soit $u_1=\frac{u_3}{q^2}$

D'ou l'équation
$\frac{u_3}{q^2}+\frac{u_3}{q}+u_3=30$ ou
$u_3(\frac{1}{q^2}+\frac{1}{q}+1)=30$

Ecris la relation ayant pour somme 120.

[Joyca Le Boss]

@Noemi q c'est la raison c'est ca ?

[Noemi]

@Joyca-Le-Boss

Oui pour une suite géométrique on note généralement $q$ pour la raison.

[Joyca Le Boss]

@Noemi Pouvez-vous m'expliquer pourquoi
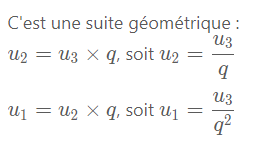
je n'ai pas compris pourquoi U2 est = U3 fois q mais pourquoi on a pas pris U1 fois q
et ensuite pourquoi U1 est = U2 fois q et ensuite divisé pas q au carré
Pouvez-vous me l'expliquer svp ?

[Noemi]

@Joyca-Le-Boss

Une erreur d'indice dans la première équation.

J'ai choisis $u_3$ car il est présent dans les deux équations.
Tu peux choisir $u_1$
Cela donne :
$u_1+u_1\times q+u_1\times q^2=30$
et
$u_1\times q^2+u_1\times q^3+u_1\times q^4=120$

[Joyca Le Boss]

@Noemi Et maintenant dois-je utiliser une formule pour trouver la raison q et U1 ?

[Noemi]

@Joyca-Le-Boss

$u_1+u_1\times q+u_1\times q^2=30$
et
$u_1\times q^2+u_1\times q^3+u_1\times q^4=120$
si on factorise $u_1$
$u_1(1+q+q^2)=30$
et
$u_1(q^2+q^3+q^4)=120$

On remarque que $4\times u_1(1+q+q^2)=4\times 30=120$.
Donc $4\times u_1(1+q+q^2)=u_1(q^2+q^3+q^4)$
On peut simplifier $u_1$
$4(1+q+q^2)=(q^2+q^3+q^4)$

Equation à résoudre.

[Joyca Le Boss]

@Noemi on doit utiliser Horner ?

[Noemi]

@Joyca-Le-Boss

Oui, applique la méthode de Horner.

[Joyca Le Boss]

@Noemi Pour Horner je multiplie par 1 ?

[Noemi]

@Joyca-Le-Boss

$4(1+q+q^2)=(q^2+q^3+q^4)$

$q^4+q^3+q^2-4q^2-4q-4=0$
soit à résoudre :
$q^4+q^3-3q^2-4q-4=0$.

Cherche les diviseurs de 4.

[Joyca Le Boss]

@Noemi je peux prendre 4 c'est bon !

[Noemi]

@Joyca-Le-Boss

Tu as :
$f(q)=q^4+q^3-3q^2-4q-4=0$.

Les diviseurs de 4, sont : -4 ; -2 ; 1 ; 2 et 4.
Tu dois trouver quel diviseur conduit à $f(q)=0$.
$f(4)=252$ donc 4 ne peut pas être choisi.

[Joyca Le Boss]

@Noemi j'ai pris -2

[Noemi]

@Joyca-Le-Boss

Oui, $f(-2)=0$
Applique Horner pour factoriser.

[Joyca Le Boss]

@Noemi j'ai trouver q3 - q2 - q - 2 = 0 Est-ce correct ?

[Noemi]

@Joyca-Le-Boss

C'est correct.

Applique une nouvelle fois Horner.

[Joyca Le Boss]

@Noemi j'ai trouver q2 + q + 1 Est-ce correct ?

[Noemi]

@Joyca-Le-Boss

Oui, si tu as choisis pour solution $q=2$.

[Joyca Le Boss]

@Noemi oui j'ai utilisé q=2

[Noemi]

@Joyca-Le-Boss

Tu poursuis avec $q^2+q+1=0$

[Joyca Le Boss]

@Noemi j'utilise egalement horner ou delta ?

[Noemi]

@Joyca-Le-Boss

L'un ou l'autre, tu dois trouver qu'il n'y a pas de solution réelle.

Tu as donc trouvé deux possibilités pour la raison 2 et -2,

Calcule le premier terme que j'ai noté $u_1$ et détermine dans chaque cas les 5 nombres.

[Joyca Le Boss]

@Noemi j'utilise 2 ou -2 pour la raison ?

[Noemi]

@Joyca-Le-Boss

Tu as deux possibilités pour cette suite donc deux solutions.
L'une en remplaçant $q$ par -2,
l'autre en remplaçant $q$ par 2.

[Joyca Le Boss]

@Noemi on utilise un des deux c'est ca ?
et je viens d'utiliser q=2 et j'ai trouver que 28=28 est-ce correct ?

[Noemi]

@Joyca-Le-Boss

Tu dois trouver une suite de 5 nombres pour chacune des valeurs de $q$.
Si $q=-2$
$u_1(1+q+q^2)=30$ donne
$u_1(1-2+4)=30$
soit
$3u_1=30$ ; $u_1= 10.
tu en déduis les 5 nombres en multipliant par -2,
soit la suite : 10 ; -20 ; 40 ; -80 ; 160.
Tu peux vérifier que :
10 - 20 + 40 = 30 et 40 - 80 + 160 = 120.

Applique le même raisonnement pour $q=2$.

[Joyca Le Boss]

@Noemi j'ai trouver 30/7 ,60/7,120/7,240/7,480/7
120/7+ 240/7+ 480/7 = 120 Est ce terminé ?

[Noemi]

@Joyca-Le-Boss

C'est juste et l'exercice est terminé.

[Joyca Le Boss]

@Noemi Merci INFINIMENT

[Noemi]

@Joyca-Le-Boss

C'est bien A+.