Exercice de Suite Géométrique !

Bonjour, Pouvez-vous m'aider a résoudre cet exercices ,J'ai fais les 3 premières et les figures ont été faite par moi-même
Voici l'exercice que j'ai commencé !

mais je n'arrive pas à faire les dernières pouvez m'aider svp ?

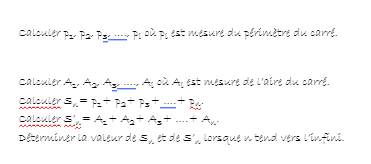
@Joyca-Le-Boss Bonjour,

Ecris l'énoncé et les questions..

@Noemi Je les ai déjà écris sur Word et ensuite je fais une capture d'écran.

@Joyca-Le-Boss

C'est illisible, écris la première question.

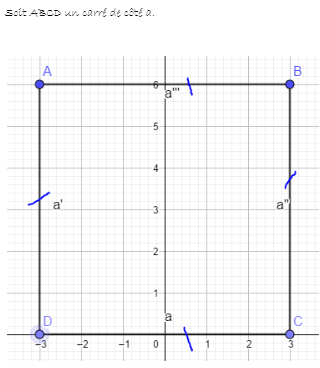
@Noemi la première question soit ABCD un carré de coté a.

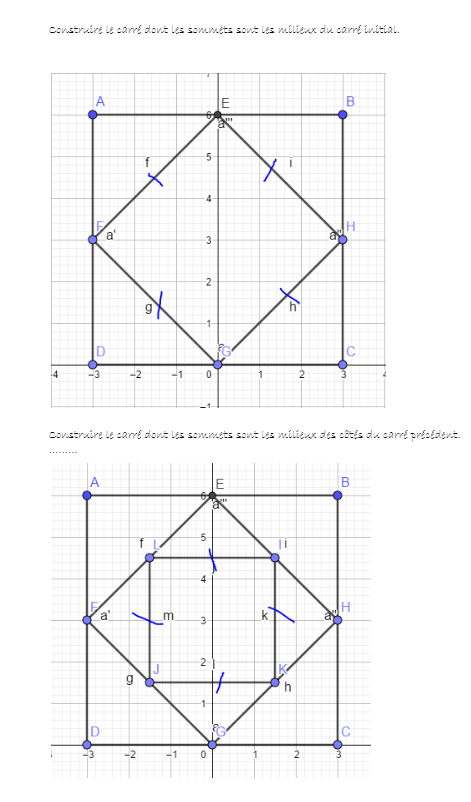
@Noemi la deuxième : Construire le carré dont les sommets sont les milieux du carré initial .
le troisième : Construire le carré dont les sommets sont les milieux du carré précédents.
et les dernières que j'ai pas réussi à faire : Calculer P2,P3,....P1+Pn.
: Calculer Sn = A1,A2,A3,....Ai ou Ai est mesure de l'aire du carré
: Calculer Sn = A1+A2+A3+....+An.
Déterminer la valeur de Sn et de S'n lorsque n tend vers l'infini.
Voila j'ai écrit tout les question.

@Joyca-Le-Boss

Le périmètre du premier carré $P_1=4a$
Pour le deuxième carré, il faut calculer la longueur d'un côté en fonction de $a$ .
Soit $a22a\dfrac{\sqrt2}{2}$ , d'ou le périmètre $P_2=....$
Pour le troisième carré, ....

@Noemi Vous avez fait comment pour trouver a racine de 2 sur 2

@Joyca-Le-Boss

Tu appliques la propriété de Pythagore $(a2)2+(a2)2=..(\dfrac{a}{2})^2+(\dfrac{a}{2})^2= ..$
ou la formule pour la diagonale d'un carré de côté $c$ : $c2c\sqrt2$

@Noemi ok et ensuite faut faire quoi svp ?

@Joyca-Le-Boss

Tu peux construire un tableau présentant le côté du carré, le périmètre puis l'aire.

$c_1 = a$ ; $P_1=4a$ ; $A_1=a^2$
$c2=a2=a22c_2= \dfrac{a}{\sqrt2}= \dfrac{a\sqrt2}{2}$ ; $P2=2a2P_2=2a\sqrt2$ ; $A2=a22A_2=\dfrac{a^2}{2}$

$c3=a2c_3=\dfrac{a}{2}$ ; $P_3=2a$ ; $A3=a24A_3=\dfrac{a^2}{4}$

Exprime chaque terme à l'ordre $n$
$C_n= ....$ ; $P_n=.....$ ; $A_n= .....$

Pour le calcul de la somme analyse les termes et détermine le type de suite.

@Noemi J'ai pas compris pourquoi vous avez divisé par la racine de 2 ?

@Joyca-Le-Boss

Pour le deuxième carré, pour calculer la longueur d'un côté, si tu appliques le théorème de Pythagore :
$(a2)2+(a2)2=2a24=a22(\dfrac{a}{2})^2+(\dfrac{a}{2})^2= \dfrac{2a^2}{4}= \dfrac{a^2}{2}$
et si tu prends la racine carrée pour calculer la longueur d'un côté :
$c=a2c=\dfrac{a}{\sqrt2}$ que l'on peut aussi écrire $a22\dfrac{a\sqrt2}{2}$ .

@Noemi le deuxième carré c'est le losange ?

@Joyca-Le-Boss

C'est un losange particulier car c'est un carré.

@Noemi et pour le troisième carré c'est la moitié du premier donc on divise par 2,Est-ce correct ?

@Joyca-Le-Boss

On relie les milieux des côtés du carré précédent. On obtient un carré. On détermine la longueur d'un côté du nouveau carré, qui est égale à la longueur du côté du carré précédent divisée par $2\sqrt2$ .

@Noemi on doit encore divisé par racine de 2 ? Pourquoi ?

@Joyca-Le-Boss

C'est le résultat.
Fais le calcul pour le troisième carré qui est construit à partir d'un carré de côté $a2\dfrac{a}{\sqrt2}$ .

@Noemi donc si on suit votre procéder ,je divise a/la racine de 2 et encore par la racine de 2 ce qui donne a/2

@Joyca-Le-Boss

Tu obtiens ainsi la longueur du côté.

Calcule le périmètre et l'aire pour chaque cas.
Fais un tableau.

@Noemi là on a trouver les formules à utiliser pour les calculer mais nous avons pas de valeur pour a ?

@Joyca-Le-Boss

Tu dois faire les calculs en laissant a.
Exemple : la première ligne du tableau
$c_1=a$ ; $P_1=4a$ ; $A_1=a^2$

@Noemi donc on doit pas trouver de nombre?

@Joyca-Le-Boss

Tu dois trouver un résultat en fonction de $a$ .

@Noemi donc a restera neutre !

@Joyca-Le-Boss

Que veux tu dire par neutre ?

@Noemi on doit trouver un nombre en fonction de a donc a et la valeur qu'on doit trouver c'est ca ?
mais ce que je n'ai pas compris c'est quel procéder devons-nous suivre pour trouver a ?

@Joyca-Le-Boss

Il n'est pas demandé de trouver $a$ , mais de calculer le périmètre, l'aire en fonction de $a$ .
Relis l'énoncé des questions.

@Noemi mais on a déjà trouver le périmètre et l'aire en fonction de a !

@Joyca-Le-Boss

Complète le tableau avec $c_2$ , $P_2$ , $A_2$
jusqu'a : $c_n$ , $P_n$ , $A_n$ .

@Noemi ok je vais essayer

@Noemi ET on commence pas par C1,P1,A1

@Joyca-Le-Boss

Oui. tu commences par les premiers termes soit $C_1$ , ....
Puis $C_2$ , ....
Puis ....

Puis tu dois en déduire $C_n$ , .....

@Noemi pourquoi ?

@Joyca-Le-Boss

J'ai indiqué $C_2$ car j'ai indiqué en exemple la réponse pour $C_1$ .

@Noemi mais j'ai pas compris comment faire ce tableau pouvez-vous me donner un indice svp

@Joyca-Le-Boss

J'ai déjà indiqué le début dans une de mes précédentes réponses.

$c_1 = a$ ; $P_1=4a$ ; $A_1=a^2$

$c2=a2=a22c_2= \dfrac{a}{\sqrt2}= \dfrac{a\sqrt2}{2}$ ; $P2=2a2P_2=2a\sqrt2$ ; $A2=a22A_2=\dfrac{a^2}{2}$

$c3=a2c_3=\dfrac{a}{2}$ ; $P_3=2a$ ; $A3=a24A_3=\dfrac{a^2}{4}$

Exprime chaque terme à l'ordre $n$
$C_n= ....$ ; $P_n=.....$ ; $A_n= .....$

Pour le calcul de la somme analyse les termes et détermine le type de suite.

@Noemi c'est une suite géométrique et pour Cn je pense qu'on doit juste remplacer a par n
Est-ce correct
,

@Joyca-Le-Boss

Dans chaque cas, tu as une suite géométrique.

pour le côtés :
$Cn=12Cn−1C_n=\dfrac {1}{\sqrt2}C_{n-1}$
Idem pour le périmètre :
$Pn=12Pn−1P_n=\dfrac {1}{\sqrt2}P_{n-1}$

Cherche la relation pour l'aire.

Dans chaque cas, tu en déduis la relation en fonction de $n$
Puis tu peux calculer la somme en utilisant la relation de la somme pour une suite géométrique.

@Noemi donc c'est ca la relation pour les cotés et les périmètre mais pourquoi c'est 1/racine de 3

@Noemi Je suis pas sur mais pour la relation de l'aire j'ai trouver 1/2 en mettant au carré. Est-ce correct ?

@Joyca-Le-Boss

Pour l'aire la raison est bien $12\dfrac{1}{2}$ .

@Noemi et la relation de l'aire c'est quoi alors ?

@Joyca-Le-Boss

Si la raison est $12\dfrac{1}{2}$ , la relation est $An=12An−1A_n= \dfrac{1}{2}A_{n-1}$ .

@Noemi l'exercice est il finis ?

@Joyca-Le-Boss

Non,

Il reste à exprimer $P_n$ et $A_n$ en fonction de $n$ .
Puis calculer la somme la somme des périmètres et des aires.

Utilise les formules du cours.

@Noemi lequel ?

@Joyca-Le-Boss

Utilise la formule pour déterminer le terme général d'une suite géométrique et pour la somme de $n$ termes d'une suite géométrique.

@Noemi la formule pour déterminer le terme général d'une suite géométrique :

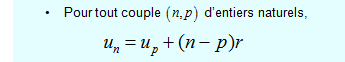
la somme de n termes d'une suite géométrique :

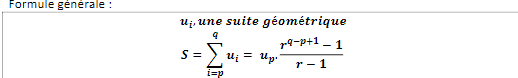
Voila les formules de mon cours

@Noemi Est-ce c'est formule ci que je dois utiliser ?

@Joyca-Le-Boss

Vérifie pour la première relation si cela correspond à une suite géométrique.

Va voir ce cours sur le site : https://www.mathforu.com/premiere-s/les-suites-en-1ere-s/

@Noemi ah oui je me suis tromper cet formule c'est celle d'une suite Arithmétique :

@Joyca-Le-Boss

Donc applique les formules.

@Noemi on a déjà exprimer Pn et An en fonction de n.
maintenant il nous reste plus cas calculer la somme des périmètres et des aires.

@Joyca-Le-Boss

Indique les résultats pour chaque termes en fonction de $n$ puis pour les sommes.

@Noemi Pour la formule de calcule de somme on doit le faire pour les 3 exercice suivant !

@Joyca-Le-Boss

Tu fais les calculs pour le périmètre et l'aire.

@Noemi Pour ces 2 là : Calculer Sn = A1,A2,A3,....Ai ou Ai est mesure de l'aire du carré
: Calculer Sn = A1+A2+A3+....+An.

@Joyca-Le-Boss

Fais les calculs.

Pour le périmètre :
$P_1=4a$ , $P2=2a2P_2=2a\sqrt2$ , ... , $Pn=4a(12)n−1P_n=4a(\dfrac{1}{\sqrt2})^{n-1}$
la somme $Sn=4a1−(12)n1−12=4a(2)n−1(2)n−1(2−1)S_n=4a\dfrac{1-(\dfrac{1}{\sqrt2})^n}{1-\dfrac{1}{\sqrt2}}= 4a\dfrac{(\sqrt2)^n-1}{(\sqrt2)^{n-1}(\sqrt2-1)}$

Applique le même raisonnement pour l'aire.

@Noemi Pouvez-vous m'expliquer comment vous êtes arriver à ce raisonnement svp ?

@Joyca-Le-Boss

J'ai juste appliqué les formules.

$Pn=P1×qn−1P_n= P_1 \times q^{n-1}$ et

$Sn=P11−qn1−qS_n= P_1\dfrac{1-q^n}{1-q}$

@Noemi ok et maintenant je fais la même chose pour l'aire c'est ca !

@Joyca-Le-Boss

Oui applique les mêmes formules.
Formules à retenir, il serait bien que tu te constitues des fiches résumées des cours.

@Noemi oui c vrai vous avez totalement raison

@Noemi A1 = a carré ,A2 = a carré / 2, A3 = a carré / 4
j'ai trouver pour An = a carré fois (1/2) exposant n-1
et Sn=a carré fois 1 - (1/2) exposant n diviser par 1-1/2 = 1-(1/2) exposant n diviser par 1/2 = 2.(1-(1/2) exposant *n)

Est -ce correct ?

@Joyca-Le-Boss

Le début est juste, il manque $a^2$ à la fin de $S'_n$ .
$Sn′=2a2(1−(12)n)S'_n=2a^2(1-(\dfrac{1}{2})^n)$ .

Il te reste la dernière question.
Calculer la limite si $n$ tend vers $+∞+\infty$ .

Pour les aires : Si $n$ tend les $+∞+\infty$ , $(12)n(\dfrac{1}{2})^n$ tend vers 0, donc $S'_n$ tend vers $2a^2$ .

Fais le même raisonnement pour $S_n$

@Noemi Sn c'est pour le périmètre ?
et (1/2) exposant n tend vers 0 car 1/2 est plus petit que 1 mais j'ai pas compris pourquoi S'n tend vers 2a carré ?

@Joyca-Le-Boss

$Sn′=2a2(1−(12)n)S'_n=2a^2(1-(\dfrac{1}{2})^n)$ .
si $n$ tend vers $+∞+\infty$ , $(12)n(\dfrac{1}{2})^n$ tend vers 0 donc $(1−(12)n)(1-(\dfrac{1}{2})^n)$ tend vers 1 et $2a2(1−(12)n)2a^2(1-(\dfrac{1}{2})^n)$ tend vers $2a^2$ .

Oui $S_n$ c'est pour le périmètre, regarde l'énoncé.

@Noemi n tend vers - ∞ ,(1/racine de 2) exposant n tend vers -1, donc Sn tend vers 4a
Est-ce correct ?

@Joyca-Le-Boss

Non, la somme des périmètres peut-elle être négative ?
Applique le même raisonnement avec $(12)n(\dfrac{1}{\sqrt2})^n$ .

@Noemi je pense que le périmètre ne peut pas être négatif donc c'est +∞

@Joyca-Le-Boss

Non plus.

$Sn=4a1−(12)n1−12S_n=4a\dfrac{1-(\dfrac{1}{\sqrt2})^n}{1-\dfrac{1}{\sqrt2}}$

Si $(12)n(\dfrac{1}{\sqrt2})^n$ tend vers 0, $S_n= .....$

@Noemi Sn tend vers 4a !

@Joyca-Le-Boss

Et non
$Sn=4a1−(12)n1−12S_n=4a\dfrac{1-(\dfrac{1}{\sqrt2})^n}{1-\dfrac{1}{\sqrt2}}$

Si $(12)n(\dfrac{1}{\sqrt2})^n$ tend vers 0,

$Sn=4a11−12=4a2(2+1)=4a(2+2)S_n=4a\dfrac{1}{1-\dfrac{1}{\sqrt2}}=4a\sqrt2(\sqrt2+1) = 4a(2+\sqrt2)$

@Noemi et donc on a finis ?

@Joyca-Le-Boss

Oui l'exercice est terminé. Il serait bien que tu reprennes tous les calculs pour bien comprendre le raisonnement.

@Noemi oui je le ferai ,merci infiniment pour votre aide !