devoir maison équation fonctionnelle
-
Romane Chevalier dernière édition par
Bonjour, je suis totalement perdue face au devoir maison que je dois rendre à la rentrée, quelqu'un pourrait-il m'aider?
voici le devoir maison en question:
-
La fonction nulle, 𝑓 = 0 sur 𝐼, est-elle solution de (𝐸) ?
-
Démontrer que si 𝑓 est solution de (𝐸), alors pour tout réel 𝑘, la fonction 𝑘𝑓 est aussi solution de (𝐸).
-
Dans cette question, on suppose que 0 ∈ 𝐼. Soit 𝑓 une solution de (𝐸).
Démontrer qu’alors, pour tout 𝑏 ∈ 𝐼 : 𝑓(𝑏) = 0 -
À l’aide de valeurs de 𝑎 et 𝑏 bien choisies, démontrer que :
𝑓(1) = 0 -
Soit 𝑎 ∈ 𝐼. On considère la fonction 𝑔𝑎 définie sur 𝐼 par :
𝑔𝑎
(𝑥) = 𝑓(𝑎𝑥) − 𝑓(𝑥)
a. Justifier que 𝑔𝑎 est une fonction constante sur 𝐼 (on précisera la valeur de cette constante).
b. Donner deux expressions de 𝑔𝑎′(𝑥) pour tout 𝑥 ∈ 𝐼.
c. En déduire que pour tout 𝑥 ∈ 𝐼 :
𝑎𝑓′(𝑎𝑥) − 𝑓′(𝑥) = 0- On pose 𝑓′(1) = 𝑘. Exprimer 𝑓′(𝑎) en fonction de 𝑘 et de a.
7.** Soit 𝑓 une fonction définie et dérivable sur 𝐼 = ]0 ; +∞[ vérifiant (𝑆). Démontrer que 𝑓 vérifie (𝐸) (on
pourra utiliser la fonction 𝑔𝑎 définie à la question 5).Je vous remercie d'avance pour vos réponses!
-
-
mtschoon dernière édition par

@Romane-Chevalier , bonjour,
Tu as dû oublier d'écrire le début de l'énoncé car on ne sait pas de quelle équation (E) il s'agit...
-
Romane Chevalier dernière édition par
@mtschoon
En effet, j'en suis désolée
Voici le début de l'énoncé:
Soit 𝐼 un intervalle. Le but de ce problème est la recherche des fonctions f, définies et dérivables sur 𝐼, qui
vérifient l’équation fonctionnelle (𝐸) suivante :
(𝐸) : pour tous 𝑎 et 𝑏 de 𝐼, 𝑓(𝑎𝑏) = 𝑓(𝑎) + 𝑓(𝑏).
Autrement dit, on recherche toutes les fonctions qui transforment les produits en sommes sur un intervalle
donné.
-
@Romane-Chevalier Bonjour,
Indique tes éléments de réponse et la question qui te pose problème.
-
Romane Chevalier dernière édition par
@Noemi
Je n'ai répondu à aucunes questions car je n'y arrive pas.
Toutes les questions me posent problèmes.
-
Si pour xxx appartenant à III, f(x)=0f(x) = 0f(x)=0
Que peut-on dire de f(a)f(a)f(a), f(b)f(b)f(b) et f(ab)f(ab)f(ab) ?
-
Romane Chevalier dernière édition par
@Noemi
je n'en ai pas la moindre idée, mon niveau est vraiment catastrophique
-
L'objectif de ce site n'est pas de faire les exercices à votre place, mais vous fournir des pistes de résolutions.
Tu es en terminale S, donc tu dois avoir quelques connaissances en mathématiques.
Qu'en on écrit f(x)=0f(x)= 0f(x)=0 cela signifie que quel que soit l'élément xix_ixi appartenant à l'intervalle III, alors f(xi)=0f(x_i)=0f(xi)=0
Donc si aaa appartient à l'intervalle alors f(a)=....f(a)= ....f(a)=....
Si bbb appartient à l'intervalle alors f(b)=...f(b)=...f(b)=...
Que peut-on dire de f(ab)f(ab)f(ab) ?
-
mtschoon dernière édition par mtschoon

Merci d'avoir compléter ton énoncé.
Pistes pour démarrer,
f étant la fonction nulle : f(a)=0f(a)=0f(a)=0 et f(b)=0f(b)=0f(b)=0 donc
f(a)+f(b)=0+0=0f(a)+f(b)=0+ 0=0f(a)+f(b)=0+0=0f étant la fonction nulle : f(ab)=0f(ab)=0f(ab)=0
donc f(ab)=f(a)+f(b)f(ab)=f(a)+f(b)f(ab)=f(a)+f(b) d'où la conclusion.
kf(ab)=k[f(a)+f(b)]=kf(a)+kf(b)kf(ab)=k[f(a)+f(b)]=kf(a)+kf(b)kf(ab)=k[f(a)+f(b)]=kf(a)+kf(b)
donc kfkfkf est aussi solution de (E).
Réfléchis à ce début .
Comme indiqué par Noemi, ici, on aide mais on ne fait pas l'exercice.
Ce n'est pas le but
Indique tes pistes pour la suite et nous t'aiderons.
-
Romane Chevalier dernière édition par
@mtschoon
Merci beaucoup pour votre réponse!
-
mtschoon dernière édition par mtschoon

Détaille bien la question 1 et la question 2
Je te mets des pistes pour la 3) et la 4) qu'il faudra expliciter.
En choisissant a=0a =0a=0
f(ab)=f(a)+f(bf(ab)=f(a)+f(bf(ab)=f(a)+f(b) donc f(0b)=f(0)+f(b)f(0b)=f(0)+f(b)f(0b)=f(0)+f(b) donc f(0)=f(0)+f(b)f(0)=f(0)+f(b)f(0)=f(0)+f(b)
Tu déduis f(b)f(b)f(b)Tu choisis a=1a=1a=1 et b=1b=1b=1 et tu utilises toujours
f(ab)=f(a)+f(b)f(ab)=f(a)+f(b)f(ab)=f(a)+f(b)Tiens nous au courant .
-
Romane Chevalier dernière édition par
@mtschoon
Merci c'est vraiment super!
-
mtschoon dernière édition par mtschoon

Pour la 4), j'espère que tu as trouvé f(1)=0f(1)=0f(1)=0
Indique tes pistes pour la 5) (si tu en as) ou indique ce qui te bloque.
Bon travail !
-
mtschoon dernière édition par mtschoon

Bonjour,
Visiblement, @Romane-Chevalier a terminé seul(e) son exercice.
Comme cet exercice semble intéressant ( et peut aboutir à utilisation du logarithme népérien), je me permet de donner des pistes pour la fin, pour consultation éventuelle.Quelques pistes pour la fin,
- a)
ga(x)=f(ax)−f(x)=f(a)+f(x)−f(x)=f(a)g_a(x)=f(ax)-f(x)=f(a)+f(x)-f(x)=f(a)ga(x)=f(ax)−f(x)=f(a)+f(x)−f(x)=f(a)
donc g est constante et a pour valeur f(a)
5)b)
En dérivant gag_aga , on obtient ga′(x)=afa′(x)−f′(x)g'_a(x)=af'_a(x)-f'(x)ga′(x)=afa′(x)−f′(x)
Vu que gag_aga est constante : ga′(x)=0g'_a(x)=0ga′(x)=05)c)
Conséquence : afa′(x)−f′(x)=0\boxed{af'_a(x)-f'(x)=0}afa′(x)−f′(x)=0En appliquant la relation qui vient d'être trouvée pour x=1x=1x=1, on obtient : af′(a)(1)−f′(1)=0af'(a)(1)-f'(1)=0af′(a)(1)−f′(1)=0
on posant f′(1)=kf'(1)=kf′(1)=k, on obtient après calcul :
f′(a)=ka\boxed{f'(a)=\dfrac{k}{a}}f′(a)=ak
7)
L'énoncé ne dit pas ce que représente (S)..... ?
Un oubli sans doute. On va essayer d' imaginer...Soit f fonction définie, dérivable sur I=]0,+∞[I=]0,+\infty[I=]0,+∞[ vérifiant f′(x)=kxf'(x)=\dfrac{k}{x}f′(x)=xk et f(1)=0f(1)=0f(1)=0
On va prouver que f transforme les produits en sommes c'est à dire que f(ax)=f(a)+f(x)f(ax)=f(a)+f(x)f(ax)=f(a)+f(x)
On utilise la fonction gag_aga définie à la question 5) comme l'indique l'énoncé.
ga(x)=f(ax)−f(x)g_a(x)=f(ax)-f(x)ga(x)=f(ax)−f(x)
ga′(x)=af′(ax)−f′(x)=a×kax−kx=kx−kx=0g'_a(x)=af'(ax)-f'(x)=a\times \dfrac{k}{ax}-\dfrac{k}{x}=\dfrac{k}{x}-\dfrac{k}{x}=0ga′(x)=af′(ax)−f′(x)=a×axk−xk=xk−xk=0Donc gag_aga est constante : ga(x)=Cg_a(x)=Cga(x)=C avec CCC constante réelle.
f(ax)−f(x)=Cf(ax)-f(x)=Cf(ax)−f(x)=C
Calculons CCC : ga(1)=f(a)−f(1)=f(a)g_a(1)=f(a)-f(1)=f(a)ga(1)=f(a)−f(1)=f(a)
Donc f(ax)−f(x)=f(a)f(ax)-f(x)=f(a)f(ax)−f(x)=f(a) , donc f(ax)=f(x)+f(a)f(ax)=f(x)+f(a)f(ax)=f(x)+f(a)
f transforme les produits en sommes donc vérifie (E)
CONCLUSION relative à l'équation fonctionnelle proposée :
Les fonctions trouvées qui transforment les produits en sommes sur l'intervalle I=]0,+∞[I=]0,+\infty[I=]0,+∞[ sont les fontions f définies, dérivables sont I, et vérifiant :
f′(x)=kxf'(x)=\dfrac{k}{x}f′(x)=xk avcc k réel et f(1)=0f(1)=0f(1)=0
- a)
-
mtschoon dernière édition par mtschoon

Complément non demandé
Nature de ces fonctions f définies à la question 7)
f′(x)=kx=k×1xf'(x)=\dfrac{k}{x}=k\times \dfrac{1}{x}f′(x)=xk=k×x1 pour x>0x \gt 0x>0
donc f(x)=kln(x)+Kf(x)=kln(x)+Kf(x)=kln(x)+K, avec KKK constante réelle.
Déterminons KKK qui vérifie f(1)=0f(1)=0f(1)=0
Vu que ln(1)=0ln(1)=0ln(1)=0,
f(1)=kln(1)+K=Kf(1)=kln(1)+K=K f(1)=kln(1)+K=K
f(1)=0f(1)=0f(1)=0 <=> K=0K=0K=0
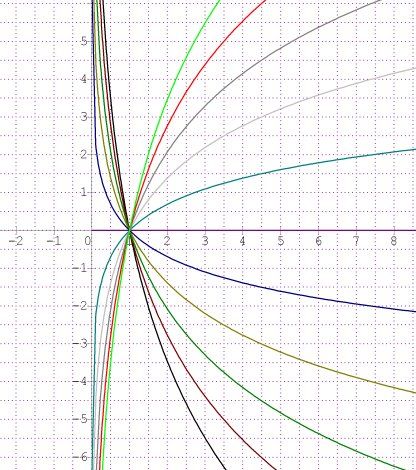
Donc, pour x>0x\gt 0x>0, avec kkk réel. f(x)=kln(x)\boxed{f(x)=kln(x)}f(x)=kln(x)Illustration graphique des fonctions f, pour k entier compris entre -5 et 5
-
Llu_lu dernière édition par
Bonjour tout le monde!
Je sais que la discussion est assez ancienne, mais j'ai pratiquement le meme dm à faire et je bloque à certains endroits...
Voici le dm:On se propose de caractériser les fonctions 𝑓 vérifiant pour tous réels 𝑎 et 𝑏 :
𝑓(𝑎𝑏) = 𝑓(𝑎) + 𝑓(𝑏) (𝐸)
ANALYSE : soit 𝒇 une fonction solution de l'équation (𝑬)
Question 1 : on suppose que 𝒇 est définie en 0.
a/ Que vaut 𝑓(0)?
b/ En déduire que pour tout réel 𝑥, 𝑓(𝑥) = 0.
Question 2 : on suppose dans toute la suite du problème que 𝒇 est définie et dérivable
sur ]𝟎; +∞[
a/ Soit 𝑎 ∈]0; +∞[. On pose pour 𝑥 ∈]0; +∞[∶ 𝑔(𝑥) = 𝑓(𝑎𝑥) − 𝑓(𝑥).
a/ Justifier que la fonction 𝑔 est une fonction constante.
b/ Donner deux expressions de 𝑔′(𝑥) pour tout 𝑥 > 0.
c/ En déduire que 𝑎𝑓′(𝑎) − 𝑓′(1) = 0.
Question 3 : détermination de 𝒇
a/ On pose 𝑓('1) = 𝑘. Exprimer 𝑓′(𝑎) en fonction de 𝑘 et de 𝑎.
b/ En déduire que pour tout 𝑥 > 0,
𝑓'(𝑥) =𝑘/𝑥.
c/ En déduire que si 𝑓 est définie et dérivable sur ]0; +∞[ et vérifie (𝐸) alors 𝑓 est d'un type
particulier. Lequel ?
SYNTHESE : soit 𝒇 une fonction définie sur ]𝟎; +∞[ par 𝒇(𝒙) = 𝑪 × 𝒍𝒏(𝒙).
Montrer 𝒇 est solution de (𝑬). Conclure en répondant au problème par une phraseJe bloque à partir de la
-
Llu_lu dernière édition par
Ce message a été supprimé !
-
Llu_lu dernière édition par
Pardon je n'avais pas fini...
je bloque à partir de la partie 3
pour la c)
pour la c), un certain type c'est à dire ? du style affine/ linéaire? Et puis pour la synthèse je suis complètement bloquée, pourriez vous me donner une piste?
Merci d'avance
-
mtschoon dernière édition par mtschoon

@lu_lu , bonjour,
C'est difficile de se replonger dans un exercice qui date d'une année...je ne sais pas si je réponds exactement à tes questions...
Type de fonction f (conclusion de l'anayse)
Pour x>0x\gt 0x>0, f(x)=kln(x)f(x)=kln(x)f(x)=kln(x), ave k constante réelle.
Tu peux dire de f est le produit de la fonction logarithme népérien par une constante réelle
Pour la synthèse
f(x)=Cln(x)f(x)=Cln(x)f(x)=Cln(x) avec C constante réelle.
f(a)=Cln(a)f(a)=Cln(a)f(a)=Cln(a)
f(b)=Cln(b)f(b)=Cln(b)f(b)=Cln(b)
f(ab)=Cln(ab)f(ab)=Cln(ab)f(ab)=Cln(ab)Tu sais que ln(ab)=ln(a)+ln(b)ln(ab)=ln(a)+ln(b)ln(ab)=ln(a)+ln(b) donc :
f(ab)=C[ln(a)+ln(b)]=Cln(a)+Cln(b)f(ab)=C[ln(a)+ln(b)]=Cln(a)+Cln(b)f(ab)=C[ln(a)+ln(b)]=Cln(a)+Cln(b)
Donc f(ab)=f(a)+f(b)f(ab)=f(a)+f(b)f(ab)=f(a)+f(b)