Distance d'un point de ln à l'origine

Bonjour, j'ai un petit problème avec mon dm de maths je vous marque l'énoncé :
Quel est le point de la représentation graphique de la fonction logarithme népérien dans un repère orthonormé (O;I;j) qui est le plus proche du repère ?
Indication : on pourra démontrer que si M(x;y) est sur la courbe représentative de ln, alors OM = √x²+(ln (x))².

Donc ce que j'ai fait, c'est que j'ai démontré que OM était la distance entre le point O et M en utilisant la formule de la distance et que le point M avait pour coordonnés (x;f(x)) or f(x)=ln(x) ici d'où ce qu'ils trouvent.
Ensuite, j'ai dit que la fonction g était égale à OM et j'ai calculé sa dérivée. Si je ne me trompe pas, g est définie sur ]0;+∞[. Ainsi, j'essaye de déterminer le signe de la dérivée qui est du signe de x + ln(x)/x car le reste est positif mais là je bloque. aussi, je ne sais pas si c'est par l'étude de signe que je trouverai les coordonnées de M mais c'était ce que je m'étais dit au début
J'aimerais bien que quelqu'un me dise si ce que j'ai fait depuis le début est juste et si oui, qu'on m'aide pour la suite merci beaucoup Screenshot_20210305-203241~3.png

@Light-Evil Bonsoir,

Le début est juste.
Etudie les variations de la fonction dérivée.

Bonsoir, je calcule donc la dérivée seconde pour trouver les variations de la dérivée ?

Sinon, j'avais essayé de trouver le signe de la dérivée et j'en ai conclu que sur ]0 ; (-1+√5)/2], g'(x) était négative donc g décroissante et sur [(-1+√5)/2 ; +∞[, g'(x) était positive donc g croissante. Du coup, je pensais que M( (-1+√5)/2 ; (-1+√5)/2 + ln( (-1+√5)/2 ) ) mais ça ne correspond pas aux coordonnées sur le graphique.

@Light-Evil

Comment as tu déterminé la valeur qui annule la dérivée ?

D'abord j'ai résolu l'inéquation x² + ln(x) > 0 et je suis tombée sur x² + x - 1 > 0. J'ai donc utilisé le discriminant en trouvant ∆=5, puis, j'ai calculé les deux racines. Puisque g est définie sur ]0;+∞[, X1 ne convient pas car X1<0 il ne reste que X2. Avec un tableau de signe, je trouve le signe de g'(x) avec X2 qui l'annule et je calcule combien vaut g(X2).

@Light-Evil

Comment passer de $x2+ln(x)>0x^2+ln(x)\gt0$ à $x2+x−1>0x^2+x-1\gt0$ ?

Tu peux trouver une valeur approchée $x = 0, 653$ .

J'ai essayé de faire comme un exercice qu'on avait fait en classe mais voilà comment j'ai trouvé ça :
x² + ln(x) > 0
e^x² + e^ln(x) > e⁰ car la fonction exponentielle croît sur R
x² + x > 1
x² + x - 1 > 0

@Light-Evil

$x^2+ln(x)$ n'est pas toujours supérieur à 0.

Oui oui, c'était pour déterminer là où cela était positif : quand j'utilise le discriminant et que je trouve 2 racines, à l'intérieur des racines x² + ln(x) est négatif car a=1>0

Je vois pas comment faire autrement, à part les coordonnées que j'ai trouvé tout à l'heure je n'arrive pas à continuer

@Light-Evil
Tu calcules la dérivée seconde . tu montres qu'elle est strictement positive sur l'intervalle de définition. La fonction variant de $−∞-\infty$ à $+∞+\infty$ , elle passe par 0.
Tu utilises le théorème des valeurs intermédiaires et tu en déduis à l'aide de la calculatrice, la valeur $x = 0, 653$ (Erreur de frappe j'ai indiqué initialement 0,753 à la place de 0,653).

Bonjour,

@Noemi a dit dans Distance d'un point de ln à l'origine :

@Light-Evil
Tu calcules la dérivée seconde . tu montres qu'elle est strictement positive sur l'intervalle de définition. La fonction variant de $−∞-\infty$ à $+∞+\infty$ , elle passe par 0.
Tu utilises le théorème des valeurs intermédiaires et tu en déduis à l'aide de la calculatrice, la valeur $x = 0, 753$ .

Je me permets d'expliciter un peu, si besoin.

Si j'ai bien lu, après transformation, la dérivée peut s'écrire:
$f′(x)=x2+ln(x)xx2+ln(x))2\boxed{f'(x)=\dfrac{x^2+ln(x)}{x\sqrt{x^2+ln(x))^2}}}$

Le signe de $f^{'} (x)$ est le signe de $g(x)=x2+ln(x)\boxed{g(x)=x^2+ln(x)}$
Tu peux utiliser les variations de g pour en déduire le signe de $g (x)$ donc de $f^{'} (x)$

$g′(x)=2x+1xg'(x)=2x+\dfrac{1}{x}$ donc $g′(x)>0g'(x)\gt 0$ pour $x>0x\gt 0$

Comme te l'a indiqué Noemi je crois, g est définie , dérivable donc continue et strictement croissante de $]0,+∞[]0,+\infty[$ vers $]−∞,+∞[]-\infty,+\infty[$
D'après le théorème de valeurs intermédiaires, il existe une valeur $α\alpha$ de $]0,+∞[]0,+\infty[$ tel que $g(α)=0\boxed{g(\alpha)=0}$

$α\alpha$ est la valeur exacte dont on ne peut trouver que des valeurs approchées

Ma calculette me donne $α≈0.653\boxed{\alpha\approx 0.653}$ , plus précisemment :
$0.652<α<0.653\boxed{0.652\lt \alpha \lt 0.653}$

( Je vois que Noemi a rectifié sa valeur - c'est bon)

Dans tes conclusions, utilise la valeur exacte nommée $α\alpha$ , ce qui sera plus correct qu'une valeur approchée.

Tu peux donner le tableau de variation de f sur $]0,+∞[]0,+\infty[$

Pour $x<αx\lt \alpha$ , $g(x)<0g(x)\lt 0$ donc $\lt 0$ donc f strictement décroissante

Pour $x>αx\gt \alpha$ , $g(x)>0g(x)\gt 0$ donc $\gt 0$ donc f ...................

Le minimum de f est pour $x = . . . . . . . .$

Bon travail !

D'accord merci beaucoup pour vos réponses et vos explications je pense avoir tout compris !

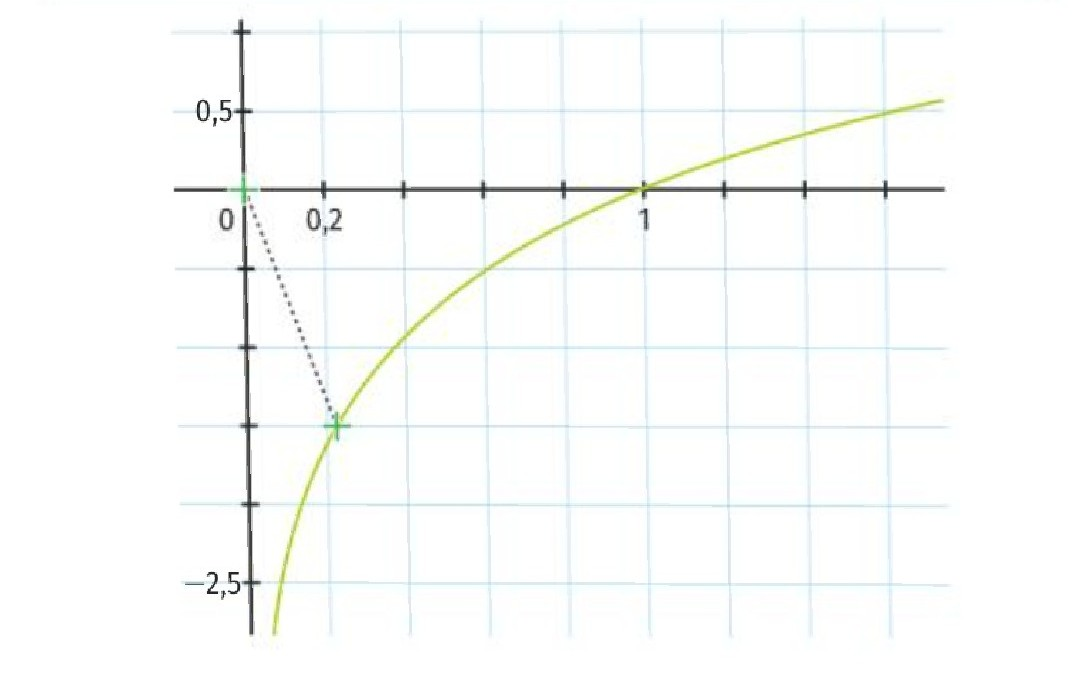
J'ai juste une dernière question, les coordonnées du point M que l'on cherche sont bien (x;ln(x)) donc le x correspond à celui de mon tableau (c'est-à-dire à a≈0,653) mais le y correspond à ln(0,653) ? Car autrement, le minimum de f est égal approximativement à 0,8 ce qui ne correspond à aucun point de la représentation graphique de ln.

Tout à fait.

Le point M est sur la courbe d'équation $y = l n (x)$ , donc M a pour coordonnées $(x, l n (x))$
La distance OM est minimale lorsque M est au point de coordonnées $(α,f(α))(\alpha, f(\alpha))$

Valeurs approchées :

$α≈0.653\alpha\approx 0.653$
$f(α)≈ln(α)≈−0.4262f(\alpha)\approx ln(\alpha) \approx -0.4262$

D'accord, c'est noté !

Je vous remercie une nouvelle fois pour vos explications qui étaient très claires, bonne journée à vous !

De rien @Light-Evil ,
Nous avons fait au mieux et c'est parfait si c'est clair pour toi.
Bon week-end à toi.