Problème Matriciel Niveau Difficile

Bonjour, Pouvez-vous m'aider à résoudre ce Problème Matriciel SVP?
Voici l'énoncé :
Une entreprise est composée de trois services A (clientèle), B (transport) et C (comptabilité) et fonctionne par rotation des employés (polyvalents) au sein de l’entreprise de la manière suivante :

du service A, 10% passe au service B, 25% passe au C et les autres restent dans le service.

du service B, 20% passe au service A, 30% passe au C et les autres restent dans le service.

du service C, 40% passe au service B, 15% passe au A et les autres restent dans le service.

Exprimer à l’aide d’une matrice 3X3 le flux de personnel au sein de l’entreprise.

Si à la création la répartition est la suivante : 100 personnes au service A, 200 personnes au service B et 60 personnes au service C, quelle sera la répartition au sein des services après 2 ans.

@Joyca-Le-Boss Re-Bonjour,

Commence par indiquer tes éléments de réponse.

La première ligne :
0,65 ; 0,10 ; 0,25

Bonsoir,

@Joyca-Le-Boss , bonsoir,

Tu cherches donc une matrice de transition

Tu peux peut-être écouter la vidéo ici qui donne un exemple qui peut t'éclairer :

https://www.youtube.com/watch?v=gmm_YF6QTlI

Bonjour,

@Joyca-Le-Boss , j'espère que tu as commencé à travailler le sujet.

Une matrice de transition peut se faire en lignes ou en colonnes.

Tout dépend de ton cours (et fais ce qui est indiqué dessus)

Noemi a complété sa réponse ( après ma proposition de vidéo qu'elle n'a pas dû regarder) en démarrant l'écriture en lignes.

La vidéo que je t'ai proposée, t'explique la méthode en en colonnes. donc je te joins une image "en colonnes".

Dans l'image que je te joins, A,B,C au départ sont en Bleu et la transition est écrite en colonnes

Si tu as compris la vidéo, tu as dû trouver pour A et B :

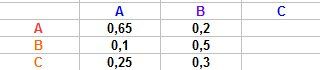
Lorsque tu as compris, tu complètes la colonne C

@Noemi Pourquoi avez-vous écrit 0,65 j'ai pas trop compris !

@Joyca-Le-Boss , nos réponses ont dû se croiser.

Je t'indique le "0.65"

100%-10%-25%=65%=1-0.1-0.25=0.65

@mtschoon ah ok et pouvons-nous le laisser en pourcentage ou pas ?

@Joyca-Le-Boss , les deux sont justes mais pour faire les calculs de la question suivante, c'est mieux en écriture décimale.

@mtschoon Pour trouver 0,1 vous avez fait 20%-30% =1 0% = 0,2-0,3=0,1 Est-ce correct
0,25 vous avez fait 40%-15%= 25 = 0,4-0,15 = 0,25

@Joyca-Le-Boss , revois ta proposition pour la colonne B

Pour B ( regarde la colonne relative à B (bleu) de l'image jointe)
l'énoncé te dit : 20% passe au service A, 30% passe au C et les autres restent dans le service.
donc , ce qui reste dans le service B est : 100%-(20%+30%)=50%=05

La colle B(beu) s'écrit donc
0.2 (ce qui passe en A)
0.5 (ce qui reste en B)
0.3 (ce qui passe en C)

@mtschoon Pour C j'ai trouver (A )-0,75 , (B) 0,2 et (c) 0,05 Est-ce correct?

L'énoncé te dit :
du service C, 40% passe au service B, 15% passe au A et les autres restent dans le service.

Je ne vois pas le lien avec ta proposition pour la colonne C.

Regarde tout ça de près.

L'énoncé n'est peut-être pas très explicite.
L'effectif global de l'entreprise de change pas (toujours 100%, si je puis dire).
C'est la répartition de cet effectif global entre les trois services (A,B,C) qui change et le total des trois service fait toujours 100%.
C'est pour cela que si un service représente 40% du total, un autre fait 15% du total, le troisième fait, en conséquence, 100%-(40%+15%).

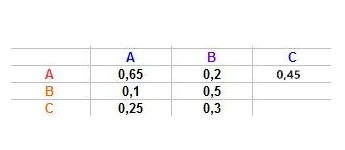
@mtschoon donc ca fait 0,45

@Joyca-Le-Boss

C'est correct.

@Noemi et ensuite que faire svp ?

@Joyca-Le-Boss

A partir de la répartition proposée et de la matrice, détermine la nouvelle répartition.
L'énoncé ne précise pas à quelle période s'effectue la nouvelle répartition.

@Noemi et c bon ca 2021-03-08 (3).png

@Noemi et les suivantes j'ai trouver 0,4 et 0,6 Est-ce correct?

@Joyca-Le-Boss

C'est faux

Pour le service C, 15% passe en A .
Complète la dernière colonne.

@Noemi c 0,5

@Joyca-Le-Boss

Visiblement tu n'as pas compris comment a été complété les deux premières colonnes.
Relis l'énoncé et propose la solution pour la troisième colonne.

@Noemi Vous pouvez me montrer tout les calculs que vous avez fait pour trouver les 2 premières colonnes svp ?

@Joyca-Le-Boss

Pour la première colonne :
L'énoncé : " du service A, 10% passe au service B, 25% passe au C et les autres restent dans le service. "
A partir des indications, on peut écrire en colonne :
A : x%
B : 10%
C : 25%

Pour calculer le pourcentage de A : 100 - 10 - 25 = 65,
Soit
A : 65%=0,65
B : 10%= 0,10
C : 25%= 0,25

Applique le même raisonnement pour les deux autres indications de l'énoncé.

@Noemi : Pour la deuxième colonne :
L'énoncé : du service B, 20% passe au service A, 30% passe au C et les autres restent dans le service.
A : 20%
B : x%
C : 30%
Pour calculer le pourcentage de B : 100 - 20- 30 = 50
Soit
A : 20%=0,2
B : 50%= 0,5
C : 30%= 0,3

ET Pour la Troisième colonne :
L'énoncé : du service C, 40% passe au service B, 15% passe au A et les autres restent dans le service.
A : 15%
B : 40%
C : x%
Pour calculer le pourcentage de C : 100 - 15 - 40= 45

A : 15%=0,15
B : 40%= 0,4
C : 45%= 0,45

Est-ce correct ?

@Joyca-Le-Boss , pour la colonne C, c'est bon maintenant.

Tu as donc maintenant la matrice de transition $T$ qui te permet de calculer la suite demandée.

$0.45)T=\begin{pmatrix}0.65\ \ \ 0.2\ \ \ 0.15\cr 0.1\ \ 0.5\ \ \ 0.4\cr0.25\ \ 0.3\ \ \ 0.45\end{pmatrix}$

Pour la suite, l'énoncé demande qu'elle sera la répartition au sein des services après deux ans , mais il a oublié d'indiquer quand a lieu les changements de répartition ! ! !

Tu peux indiquer que tu as supposé que le changement de répartition a lieu tous les ans , à partir de la création donnée, et faire ainsi le calcul.

@Joyca-Le-Boss , bonjour,

Une indication si besoin , pour la suite.

Soit $A$ la matrice colonne représentant la répartition lors de la création

$A=(10020060)A=\begin{pmatrix}100\cr 200 \cr 60\end{pmatrix}$

Un an après, la répartition est $B=T×AB=T\times A$

Tu cherches la répartition deux ans après.

Tu peux donner ta réponse si tu souhaites une vérification.

@mtschoon et j'ai pas compris comment je dois répondre a cet question
Si à la création la répartition est la suivante : 100 personnes au service A, 200 personnes au service B et 60 personnes au service C, quelle sera la répartition au sein des services après 2 ans.
Pouvez-vous me donner un indice svp !!

@mtschoon je dois les multiplier
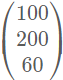2021-03-09 (3).png X 2021-03-09 (5).png = .....
EST-CE COMME CA ?

@Joyca-Le-Boss , je t'ai donné un indice, mais il faut que tu comprennes le principe.

Un an après la création, $A$ étant la répartition de départ , la répartition est $\times A$

Tu calcules $B$ (c'est le calcul matriciel que tu as positionné)

Deux ans aprés la création, la nouvelle répartition est $C$ :
$C=T×BC=T\times B$

Tu calcules $C$ qui est la répartition demandée

Tu pourrais faire un calcul différent pour trouver C sans passer par $B$ ( méthode justifiée par le fait que la multiplication matricielle est associative)

$C=T2×AC=T^2\times A$

Tu peux faire les deux procédés pour vérifier que tu trouves pareil pour $C$

Une remarque ( non demandée)
Si on t'avait demandé la répartition $D$ au bout de 3 ans , tu aurais continué le même principe :
$D=T×CD=T\times C$ ou bien $D=T3×AD=T^3\times A$

Bons calculs.
Tu peux donner ton résultat pour vérification si tu le souhaites.

@mtschoon on doit mettre toute la matrice T au carré ou on doit la multiplier par elle et ensuite multiplier par A ?

@Joyca-Le-Boss , nos messages se sont croisés...

Revois mes propositions tranquillement.
Je pense que tout est indiqué.
Tu as deux méthodes pour trouver C ;
Tu en fais une de deux (ou les deux pour vérifier que tu trouves pareil pour C)

Elever une matrice au carré veut dire la multiplier par elle-même
$T2=T×TT^2=T\times T$

@mtschoon mais je comprend que veut dire le T carré ? ca veut dire que je dois mettre la matrice T au carré ?

@Joyca-Le-Boss ,
Je viens de te le dire...
$T^2$ est la matrice que l'on obtient en faisant le calcul $\times T$

@mtschoon ah ok merci

@mtschoon J'ai trouver B= 2021-03-09 (8).png
Est-ce correct ?

@Joyca-Le-Boss
Oui pour $114$ et $112$
$74$ ne me semble pas exact

@mtschoon ah oui c'est 134 désolé

@Joyca-Le-Boss ,
Oui, c'est $134$

@mtschoon et pour trouver C j'ai utiliser C=T x B ET j'ai trouver 2021-03-09 (11).png
Est-ce correct ?

@Joyca-Le-Boss ,

OUI !

@Joyca-Le-Boss ,

Une remarque pour faire une vérification.

Le nombre d'employés est $100 + 200 + 60 = 360$

Cette somme est constante.
Donc, quelle que soit la répartition, elle doit valoir 360

Tu peux donc t'assurer , pour la répartition au bout d'un an que :
$114 + 134 + 112 = 360$
et que, pour la répartition au bout de deux ans que
$117.7 + 123.2 + 119.1 = 360$

Si la somme ne vaut pas 360, cela prouve qu'il y a une erreur quelque part.
Tu aurais ainsi pu voir que le $74$ proposé était faux car $114 + 74 + 112 = 300$ et non $360$ .
Evidemment, si la somme vaut 360, cela prouve qu'il n'y a pas d'erreur apparente (mais bien sûr, il peut y avoir des erreurs qui se neutralisent...)

@Noemi Pouvez-vous m'aider à résoudre un exercice en physique svp !

https://forum.mathforu.com/topic/31746/exercice-mrua-de-physique