Logarithme népérien exercice
-
Rania Belaidouni dernière édition par
Bonjour j'ai un peu de mal avec un exercice:
La fonction f est définie et deux fois dérivable sur l'intervalle [0,5;5] par f(x)=(5+5ln(x))/x
a ) Calculer la dérivée et la dérivée seconde.
Donc pour cela je n'ai pas eu de gros problème:
f'(x)=(5X(1/x)Xx-x²X5+5ln(x) /x²
f'(x)=-5x+10xXln(x)/x^4b)Déterminer une équation de la tangente à la courbe Cf au point d'abscisse e.
Voila je ne parviens pas à faire cette question.f"(x)= -5X (1/x) Xx²-2xX-5ln(x) /x^4
f"(x)= -5x+10xXln(x) /x^4
-
@Rania-Belaidouni Bonjour,
Vérifie les calculs de la dérivée :
f′(x)=5x×x−5−5ln(x)x2=−5ln(x)x2f'(x) = \dfrac{\dfrac{5}{x}\times x-5-5ln(x)}{x^2} = -\dfrac{5ln(x)}{x^2}f′(x)=x2x5×x−5−5ln(x)=−x25ln(x)Pour la dérivée seconde, tu peux simplifier par xxx.
Pour l'équation de la tangente :
$y=f'(e)(x-e)+f(e)
Tu peux calculer séparément f(e)f(e)f(e) et f′(e)f'(e)f′(e).
-
mtschoon dernière édition par mtschoon

Bonjour,
@Rania-Belaidouni , je t'indique des résultats pour vérifications éventuelles.
Pour la dérivée seconde, en dérivant f′(x)f'(x)f′(x) et en simplifiant par x , tu dois trouver :
f′′(x)=10ln(x)−5x2f''(x)=\dfrac{10ln(x)-5}{x^2}f′′(x)=x210ln(x)−5
Sachant que ln(e)=1ln(e)=1ln(e)=1 , tu ne dois pas avoir de difficulté pour trouver l'équation de la tangente.
Après simplifications, elle peut s'écrire :
y=−5e2x+15ey=-\dfrac{5}{e^2}x+\dfrac{15}{e}y=−e25x+e15Graphique pour illustrer :
La courbe est en bleu ( de A à B ) et la tangente (au point C d'abscisse eee) est en rouge.
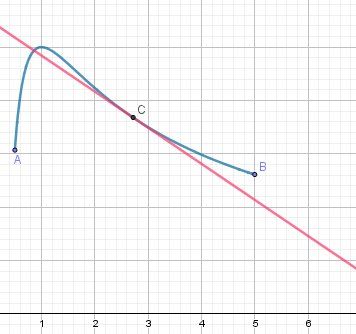
Reposte si besoin.
-
Rania Belaidouni dernière édition par
Merci beaucoup, j'ai pu finir mon exercice.
-
C'est très bien.
-
mtschoon dernière édition par

Bravo !