Fonction, équation dans un autre repère

Bonjour
j ai des difficultés à trouver l équation cartésienne d une fonction dans un autre repère .
f(x)=(2x^2-7x+8)/(x-2)
on désigne Cf sa courbe représentative dans le plan rapporte à un repère orthonormé (o,i,j)
soient le point I(2,1) et le vecteur u=i+2j
Ecrire une équation cartésienne de Cf dans le repère (I,u,j)

@Mariem-jabloun Bonjour,

Vérifie l'énoncé.

Bonjour,

@Mariem-jabloun , tu dois avoir les formules de changement de repère dans ton cours.
Si besoin, je te les indique.

Repère $\overrightarrow{i}, \overrightarrow{j}$ : $y = f (x)$

Repère $\overrightarrow{U}, \overrightarrow{V})$ : $Y = g (X)$
avec :

$I(x_0,y_0)$
$U→=ai→+bj→\overrightarrow{U}=a\overrightarrow{i}+b\overrightarrow{j}$
$V→=ci→+dj→\overrightarrow{V}=c\overrightarrow{i}+d\overrightarrow{j}$

FORMULES:
$x=aX+cY+x0\boxed{x=aX+cY+x_0}$
$y=bX+dY+y0\boxed{y=bX+dY+y_0}$

Si j'ai bien lu, dans ton énoncé :
$y=2x2−7x+8x−2y=\dfrac{2x^2-7x+8}{x-2}$
$x_0=2$
$y_0=1$
$a = 1$
$b = 2$
$c = 0$
$d = 1$

Tu remplaces x et y en fonction de X et Y :

$2X+Y+1=2(X+2)2−7(X+2)+8X2X+Y+1=\dfrac{2(X+2)^2-7(X+2)+8}{X}$

Tu isoles Y :
$Y=2(X+2)2−7(X+2)+8X−X−1Y=\dfrac{2(X+2)^2-7(X+2)+8}{X}-X-1$

Tu améliores au mieux le membre de droite.

Bons calculs.

@Mariem-jabloun , au cas où la démonstration ne serait pas claire dans ton cours, je te mets celle-ci :

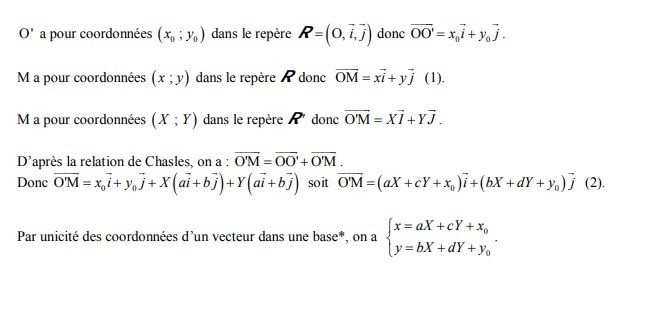
Bien sûr, si les formules de changement de repère ne font pas partie de ton cours, tu peux faire le calcul, avec la démonstration proposée, avec les données de ton énoncé.

Bons calculs.

@mtschoon
merci beaucoup pour les formules

De rien @Mariem-jabloun et bon travail.