Fonction, limites, continuité et dérivabilité

J'ai besoin d'une correction pour cet exercice

Scan supprimé par la modération.

@Mariem-jabloun , bonjour,

Ici, les scans d'énoncés ne sont pas autorisés (sauf pour tableaux ou graphiques).

Je pense que la modération supprimera le tien.

Merci d'écrire l'énoncé à la main, avec les éléments de réponses que tu as trouvés et tu auras de l'aide.

soit la fonction f définie sur R par: (2x^2-2x-4)/(x^2-1) si x<-1
(√(x^2+3)-2)/(x-1) si -1<=x<1
√(4x^2+2x-6)-ax si x=>1
on désigne par Cf sa courbe représentative dans le plan muni d'un repère orthonormé (o,i,j)
1)calculer lim f(x) lorsque x tend vers -∞ interpréter graphiquement le résultat obtenu.
2)a/étudier la continuité de f en - 1
b/déterminer la valeur de a pour que f soit continue en 1.
3)on prend dans toute la suite a= 1
a/calculer les limites de f(x) lorsque x tend vers +∞.
b/montrer que la droite D d'équation y = x + 1 / 2 et une asymptote oblique a Cf au voisinage de +∞.
c/étudier la position relative de Cf et la droite D sur [1,+∞[
4)étudier la dérivabilité de f en 1, interpréter graphiquement les résultats obtenus.
5)soit x' ∈]1,+∞[
a/calculer f'(x')
b/existe-t-il une tangente à Cf parallèle à la droite D1 :y = x+ 2015
c/ existe-t-il une tangente à Cf perpendiculaire à la droite D1 :y= x + 2015

@Mariem-jabloun Bonjour,

Il manque tes éléments de réponse et l'indication de la ou les questions qui te posent problème.

Rebonjour @Mariem-jabloun ,

Si tu n'as pas démarré, je regarde la question 1)

Vu que l'on te demande la limite en $−∞-\infty$ , tu utilises l'expression de f(x) valable pour $x<−1x\lt -1$ c'est à dire :
$f(x)=2x2−2x−4x2−1f(x)=\dfrac{2x^2-2x-4}{x^2-1}$
Si la propréité est dans ton cours, tu peux prendre la limite des termes de plus fort degré (sinon, tu mets $x^2$ en facteur au numérateur et au dénominateur et tu simplidifies par $x^2$ )

$lim⁡x→−∞f(x)=lim⁡x→−∞2x2x2=2\displaystyle\lim_{x\to -\infty}f(x)=\displaystyle{\lim_{x\to -\infty}\dfrac{2x^2}{x^2}=2}$

Tu tires la conclusion graphique.
Essaie de poursuivre et donne tes débuts de réponses.

Mon problème est que la valeur de a que j'ai trouvée telle que f soit continue en 1 ne correspond pas à 1 comme l'indique la suite de l'exercice

@Mariem-jabloun ,

As-tu trouvé une valeur de a telle que f soit continue en 1 ? laquelle ?
Merci de l'indiquer.

Remarque : Rien ne prouve que la valeur a de la question 2)b) soit la valeur a=1 de la question 3) et des suivantes.

@mtschoon
pour étudier la dérivabilité de f en 1(question 4) ,elle doit être continue en 1 d abord

@mtschoon
j ai trouvé a=-1/2

@Mariem-jabloun ,

Oui, c'est bien $a=−12a=-\dfrac{1}{2}$ pour la question 2)b)

Attention à la relation entre dérivabilité et continuité.

Si une fonction est dérivable, elle est continue.

Par contre, si une fonction est continue, elle n'est pas forcément dérivable.

Un exemple : la fonction valeur absolue.
Elle est continue en 0 mais elle n'est pas dérivable en 0.

Si une fonction n'est pas continue en $x_0$ , elle n'est pas dérivable en $x_0$ mais il peut y avoir , par exemple , un nombre dérivé à droite et un nombre dérivé à gauche ( différents l'un de l'autre ).

@mtschoon
mais ce n est pas logique de poser une question sur la dérivabilité d une fonction en un réel et elle n est pas continue en ce réel.Est-ce vrai?
Et merci d'avoir confirmé la valeur de a ;j ai douté que ma réponse soit fausse

@Mariem-jabloun ,

Oui, vu que la fonction n'est pas continue en 1, donc elle n'est pas dérivable en 1 (et on pourrait s'en arrêter là), mais je pense que l'énoncé veut te faire étudier la dérivabilité à droite et la dérivabilité à gauche, bien que la fonction ne soit pas dérivable en $x_0=1$ .
C'est l'énoncé qui décide...

@Mariem-jabloun

mais ce n est pas logique de poser une question sur la dérivabilité d une fonction en un réel et elle n est pas continue en ce réel

Pourquoi ne pas pouvoir poser la question ?

Comme la fonction n'est pas continue en 1 (avec a = 1) et bien la fonction n'est pas dérivable en 1 ... tout simplement.

Bonjour,

@Mariem-jabloun ,

Bien sûr, comme déjà indiqué, tu peux commencer par dire que, vu que $a≠−12a\ne-\dfrac{1}{2}$ , la fonction n'est pas continue en $x_0=1$ , donc elle n'est pas dérivable en $x_0=1$ .

Mais comme l'énoncé te demande d'interpréter graphiquement les résultats obtenus, tu dois "creuser" pour savoir ce qui se passe, pour la dérivabilité, à droite et à gauche.

Idée,
$f(1)=0−1=−1f(1)=\sqrt{0}-1=-1$

Etude de la dérivabilité à gauche
tu dois chercher
$lim⁡x→1−f(x)−f(1)x−1=lim⁡x→1−(x2+3−2x−1+1)×(1x−1)\displaystyle \lim_{x\to 1^{-}}\dfrac{f(x)-f(1)}{x-1}=\lim_{x\to 1^{-}}\biggr(\dfrac{\sqrt{x^2+3}-2}{x-1}+1\biggr)\times\biggr(\dfrac{1}{x-1}\biggr)$

Etude de la dérivabilité à droite
tu dois chercher
$lim⁡x→1+f(x)−f(1)x−1=lim⁡x→1+(4x2+2x−6−x+1)×(1x−1)\displaystyle \lim_{x\to 1^{+}}\dfrac{f(x)-f(1)}{x-1}=\lim_{x\to 1^{+}}\biggr(\sqrt{4x^2+2x-6}-x+1)\times\biggr(\dfrac{1}{x-1}\biggr)$

@Mariem-jabloun , je viens de faire les calculs.

Sauf erreur, à droite, la limite cherchée est $+∞+\infty$ , et à gauche elle est $−∞-\infty$

Donc, pour x=1, tangente (je devrais plutôt dire deux demi-tangentes) parallèle à l'axe des ordonnées (équation x=1)

@Mariem-jabloun ,

Illustration graphique a=1

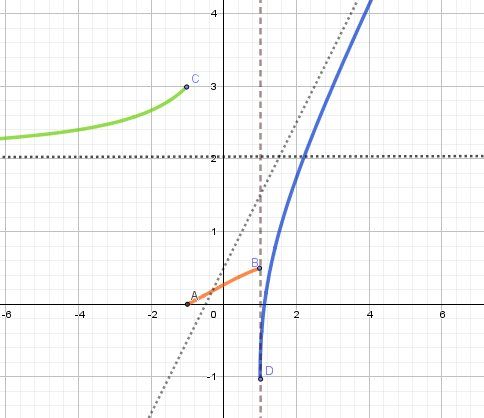
dérivabilité.jpg

Fonction f représentée en vert, rouge, bleu
Point C non pris, point A pris, point B non pris, point D pris.
Les asymptotes trouvées sont en pointillés courts noirs
La tangente verticale au point D est en pointillés longs noirs.

Tant que j'y suis , je regarde la 5)

Pour $\gt 1$ , tu n'as pas eu de difficultés je pense pour le calcul de $f^{'} (x^{'})$

Tangente parallèle à (D1) <=> $f^{'} (x^{'}) = 1$ ( coefficients directeurs égaux).
Par élévation au carré, on obtient une équation du second degré impossible.

Tangente perpendiculaire à (D1) <=> $f^{'} (x^{'}) = - 1$ ( le produit des coefficients directeurs doit valoir -1).
Une solution $x′=−14x'=-\dfrac{1}{4}$

Bon travail.