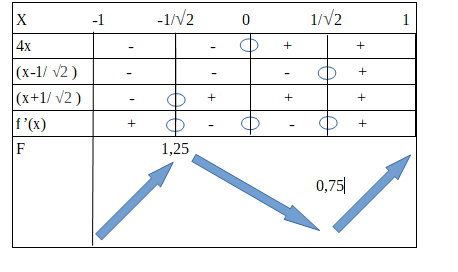
Exercice variations de fonction

Bonjour dans un exercice j'ai cet énoncé:
Soit f(x) = x^4 - x² + 1
Déterminer le tableau de variation de f

J'ai fait ça:

![text alternatif]( url de l'image)

Est-ce quelqu'un peut me dire si c'est juste. Merci de votre aide
Et ce que quelqu'un connaît un générateur de tableau de variation autre que latex?

Bonjour,

f'(x) = 2x(2x²-1)
f'(x) = 4x.(x² - 1/2)
f'(x) = 4x.(x² - (1/V2)²) (avec V pour racine carrée)
f'(x) = 4x.(x - 1/V2).(x + 1/V2)

Avec cela, corrige ton tableau

D'accord merci pour la réponse j'ai oublié de préciser que f est défini sur [-1,1]

@Black-Jack Ducoup j'ai juste à ajouter -V1/2 dans la ligne x et à mettre 4x au lieu de 2x ?

@mireille-b Bonsoir,

Tu dois étudier le signe de la dérivée selon chaque intervalles.
Donc rectifie le tableau de variations.

Bonjour,

Oui @mireille-b,

Tu dois mettre :
une ligne pour x avec les valeurs $1-1\ , \ -\dfrac{1}{\sqrt 2}, \ 0\ ,\ \dfrac{1}{\sqrt 2}\ , \ 1$
une ligne pour $4 x$ , qui s'annule pour $x = 0$
une ligne pour $(x−12)(x-\dfrac{1}{\sqrt 2})$ , qui s'annule pour $x=12x=\dfrac{1}{\sqrt 2}$
une ligne pour $(x+12)(x+\dfrac{1}{\sqrt 2})$ , qui s'annule pour $x=−12x=-\dfrac{1}{\sqrt 2}$
une ligne pour le signe de $f^{'} (x)$
une ligne pour f

@mireille-b , si tu veux avoir une idée du sens de variations de f sur $[- 1, 1]$ , je te joins une image de la représentation graphique de f
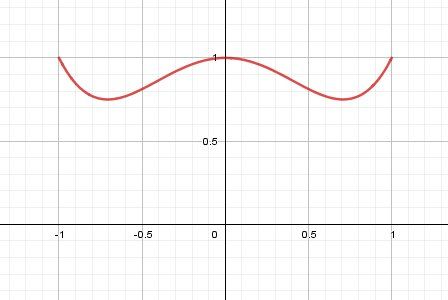
Fonctionx^4.jpg

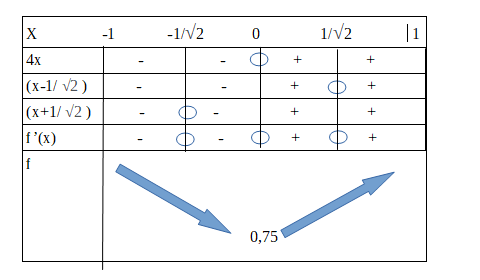
@mtschoon J'ai modifié ducoup est ce que c'est juste?

Il y a des erreurs, @mireille-b

La ligne relative à x est juste

La ligne relative à 4x est juste

Il y a une erreur de signes sur la ligne relative à $(x−12)(x-\dfrac{1}{\sqrt 2})$
$x−12>0x-\dfrac{1}{\sqrt 2} \gt 0$ <=> $x>12x\gt \dfrac{1}{\sqrt 2}$ (signe +)
$x−12<0x-\dfrac{1}{\sqrt 2} \lt 0$ <=> $x<12x\lt \dfrac{1}{\sqrt 2}$ (signe -)

Il y a une erreur de signes sur la ligne relative à $(x+12)(x+\dfrac{1}{\sqrt 2})$
$x+12>0x+\dfrac{1}{\sqrt 2} \gt 0$ <=> $x>−12x\gt -\dfrac{1}{\sqrt 2}$ (signe +)
$x+12<0x+\dfrac{1}{\sqrt 2} \lt 0$ <=> $x<−12x\lt -\dfrac{1}{\sqrt 2}$ (signe -)

Commence par comprendre cela.

Ensuite tu en déduis, par colonne, le signe de $f^{'} (x)$ (règles des signes d'un produit)

Enfin,
lorsqu'il y a un signe + à $f^{'} (x)$ , il y a une flèche qui monte pour f
(f croissante)
lorsqu'il y a un signe - à $f^{'} (x)$ , il y a une flèche qui descend pour f
(f décroissante)

Ainsi, les flèches que tu obtiens pour f sont conformes à la représentation graphique de f

@mireille-b Bonjour,

Les deux premières lignes du tableau sont justes.
Les autres lignes sont à rectifier.

@Noemi , bonjour,

Nous avons posté en même temps ( mais j'ai été plus explicite...)

@mtschoon Bonjour,

Pas de problème, je n'avais pas vu que tu étais en ligne.

Ce message a été supprimé !

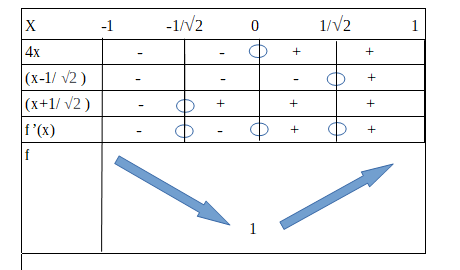
@mtschoon Merci pour vos rectifications. J'espère que c'est la bonne cette fois

@mireille-b ,
C'est mieux, mais ce n'est pas encore exact.

Les 4 premières lignes sont exactes.

Il y a deux signes faux dans la ligne de f'(x) .
Comme déjà dit, utilise la règle des signes d'un produit .

En conséquence les flèches de f ne sont pas bonnes (et pas conformes à le représentation graphique que je t'ai donnée)

@mtschoon

@mireille-b , ce n'est pas encore bon.

J'essaie de te détailler les signes de f'(x) , car tu as deux signes faux.

Dans la colonne de gauche , il y a les trois facteurs négatifs ( 3 signes -)
donc f'(x) est négative (signe -)

Dans la colonne suivante, il y a deux facteurs négatifs et un facteur positif, donc f'(x) est négative (signe +)

Les signes de f'(x) relatifs aux deux dernières colonnes sont exacts.

Donc rectifie les signes de f'(x) et les flèches de f.

@mireille-b , pour les valeurs particulières à mettre, tu dois trouver après calculs :
$f (- 1) = f (1) = f (0) = 1$
$f(−12)=f(12)=34=0.75f(-\dfrac{1}{\sqrt 2})=f(\dfrac{1}{\sqrt 2})=\dfrac{3}{4}=0.75$

Ce message a été supprimé !

@mireille-b , cette fois , c'est exact , sauf la valeur de $f(−12)f(-\dfrac{1}{\sqrt 2})$ que je t'ai indiquée.

Ce 1.25 n'a guère de sens car on ne peut pas avoir un minimum de 1.25 avec un maximum de 1 ...

@mtschoon Ok merci d'avoir pris le temps de m'aider!

De rien @mireille-b , c'est parfait si tu as bien compris.

Ce message a été supprimé !

Ce message a été supprimé !

@mireille-b

Pour un nouveau exercice, ouvre un autre sujet.

Bonjour,

@mireille-b , comme te l'a indiqué Noemi, ici :
un exercice=une discussion

Tu dois ouvrir une autre discussion pour ton second exercice, si tu as besoin d'aide.

Tu pourras en profiter pour vérifier l'énoncé donné, car l'équation de la parabole n'est pas indiquée. Est-ce normal ?Cela semble être $y=-x^2+1$ , mais ce n'est pas écrit...

Mais, cet exercice n'est-il pas la suite de cet exercice avec la fonction f définie par $f(x)=x^4-x^2+1$ dont tu viens d'étudier les variations ?

Tout cela n'est pas clair.

Il faut donner des précisions.

@mtschoon Ok merci et oui l'équation était bien celle que vous avez citer

@mireille-b , alors, en réalité, il s'agit du même exercice .

Je regarde ta question.

$OK^2=(x_K-x_O)^2-(y_K-y_O)^2$

K est sur la parabole, donc a pour coordonnés $x,-x^2+1)$

Donc

$OK^2=(x-0)^2+(y-0)^2$

$OK^2=(x-0)^2+(-x^2+1-0)^2=x^2+(-x^2+1)^2$

Il te reste à developper l'identité remarquable sans faire d'erreur.

Pour que ça soit plus simple, tu peux écrire :

$OK^2=x^2+(1-x^2)^2$

Après développement de $1-x^2)^2$ , tu dois trouver :

$OK^2=x^4-x^2+1$

C'est à dire $OK^2=f(x)$

Reposte si tu n'y arrives pas.

@mireille-b , tu viens d'effacer l'énoncé de ta question complémentaire ???

Je reste perplexe...

J'indique sommairement de quoi il s'agit pour cette question complémentaire pour que ceux qui consultent puissent comprendre :
K est un point de la parabole d'équation $y=-x^2+1$ , (pour $x∈[−1,1]x\in[-1,1]$ )
Prouver que $OK^2=f(x)$

@mtschoon Bonjour oui je l'avais effacé pour la reposter comme c'est un exercice par post mais en effet c'était la suite de l'exercice que vous m'avez aidé à traiter

Bonjour @mireille-b ,

Pas de problème !
Effectivement , il y a eu confusion vu que ta dernière question n'était pas un nouveau sujet mais la suite de ton exercice.
J'espère que tu as bien compris l'aidé donnée à cet exercice.

Bonne journée.