Intersection avec les axes

Bonsoir,
Quelqu'un pourrait m'aider à trouver comment faire l'intersection de la courbe avec les axes , pour les fonctions comportant le logarithme népérien et les fonctions polynôme

@Simaths Bonjour,

Indique la fonction.
Pour l'intersection avec l'axe des abscisses , tu résous l'équation $y = 0$ .
Pour l'intersection avec l'axe des ordonnées , tu utilises le fait que $x = 0$ .

Bonjour,
@Simaths , si un exemple t'intéresse, tu peux regarder ici :
https://www.youtube.com/watch?v=s9qUj2kkUOk

Bien sûr, comme te l'a indiqué Noemi, si c'est une fonction particulière que tu veux traiter, indique la fonction.

@Noemi je parle des fonctions comportant les polynôme et logarithme népérien
Exemple :f(x)= x-1+ln(3-x)
J'arrive pas à résoudre pour y=f(x)=0

@Simaths

L'énoncé comporte t-il des questions avant celle-ci. par exemple étude de la fonction ?

@Noemi oui, la question était d'étudier la fonction, j'ai fini de faire l'étude, maintenant le problème se pose sur l'intersection avec les axes

@Simaths , tu as dû voir le théorème des valeurs intermédiaires en cours.

Je pense que tu as trouvé:
$Df=]−∞,3[D_f=]-\infty,3[$
f strictement croissante sur $]−∞,2[]-\infty,2[$
f strictement décroissante sur $] 2, 3 [$
maximum pour $x = 2$ : $f (2) = 1$

D'après le TVI,
f est définie, continue et strictement croissante de $]−∞,2[]-\infty,2[$ vers $]−∞,1[]-\infty,1[$
$0∈]−∞,1[0\in ]-\infty,1[$
Il existe donc une valeur unique $α\alpha$ de $]−∞,2[]-\infty,2[$ telle que $f(α)=0\boxed{f(\alpha)=0}$
A la calculette, $α≈−0.15\boxed{\alpha\approx -0.15}$

Tu raisonnement de la même manière sur l'intervalle $] 2, 3 [$ où tu trouveras une valeur $β\beta$ telle que $f(β)=0f(\beta)=0$
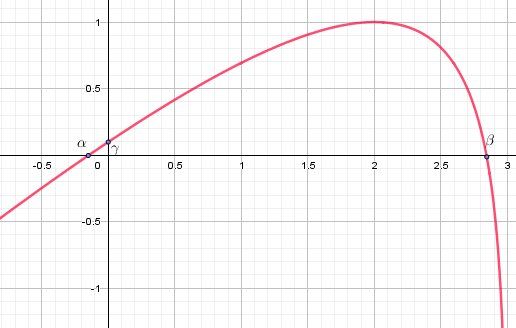
(Tu dois trouver $β≈2,85)\beta \approx 2,85)$

La représentation graphique de f coupe l'axe des abscisses aux points de coordonnées $(α,0)(\alpha,0)$ et $(β,0)(\beta,0)$

@Simaths ,

Pour l'intersection de la courbe avec l'axe des ordonnées : c'est simple
$f (0) = - 1 + l n (3)$

La représentation graphique de f coupe l'axe des abscisses au point de coordonnées $(0, - 1 + l n (3))$
$−1+ln(3)≈0.098-1+ln(3)\approx 0.098$

Bon travail !

Représentation graphique

$α≈−0.15\alpha \approx -0.15$
$β≈2.95\beta \approx 2.95$
$γ≈0.098\gamma \approx 0.098$

@mtschoon je veux savoir si sans la calculette on peut trouver une solution

@Simaths ,

Dans cet exercice, il n'est pas possible de trouver les valeurs numériques exactes solutions de $f (x) = 0$

C'est pour cela que l'on utilise le TVI et que les solutions exactes s'appellent, par exemple, $α\alpha$ et $β\beta$

Ensuite, c'est avec la calculette que l'on trouve leurs valeurs approchées.

@Simaths
salut peu tu stp detailler le calcul du domaine de definition!

@loicstephan ,

La condition d'existence est liée au logarithme :
$3−x>03-x\gt 0$ <=> $−x>−3-x\gt -3$ <=> $x<3x\lt 3$

donx $Df=]−∞,3[D_f=]-\infty,3[$

@mtschoon mtschoon j'avais voulu savoir comment avez vous résolu l'équation f(x)=0, s'il vous plaît avec beaucoup d'explication

@Simaths

Pour le calcul, utilises ta calculatrice.
En utilisant le graphe, la résolution donne $x_1=-0,14619...$ et $x_2=2,8414...$
Tu peux utiliser la technique par balayage.
Pour la première solution elle est comprise entre $- 0, 5$ et $0$ .
Et la deuxième solution entre $2, 5$ et $3$ .
Quelle calculatrice as-tu ?

@Noemi c'est une marchine powercalc, merci beaucoup d'avance mais pouvez-vous m'aider

@Simaths

Utilise le tableau de valeurs de la fonction en modifiant le pas.

Bonjour,

@Simaths , powercalc, je ne connais pas...

Eventuellement, tu peux poser ta question dans la catégorie "Math-outils" où tu trouves la sous-rubrique "Calculatrices"
(pour le cas où une personne ayant cette calculette puisse te répondre)

Bien sûr , tu as, au départ, une idée des valeurs aprochées à trouver avec la représentation graphique de la fonction obtenue sur ta calculette.

A tout hazard, je t'indique la méthode pour ma TI.
Vois si cette méthode peut être appliquée à la tienne, avec quelques modifications...

a) J'ai la touche Y où je mets l'expression de la fonction (c'est à dire x-1+ln(3-x))

b) Ensuite je vais à TblSet (table setup)
où j'indique
la valeur de x de départ (tblStart) : -0.2 par exemple
la valeur du pas (Delta tbl) : 0.01 par exemple

c) Enfin, je vais à TABLE
Là , j'obtiens deux colonnes remplies
une pour x
une pour y
Avec les flèches (montante et/ou descendante), j'obtiens les valeurs souhaitées.
Pour x=-0.15, $y≈−0.0026y\approx -0.0026$
Pour x=-0.14, $y≈0.00422y\approx 0.00422$
Donc : $\lt \alpha \lt -0.14$

@mtschoon a dit dans Intersection avec les axes :

@loicstephan ,

La condition d'existence est liée au logarithme :
$3−x>03-x\gt 0$ <=> $−x>−3-x\gt -3$ <=> $x<3x\lt 3$

donx $Df=]−∞,3[D_f=]-\infty,3[$
bonjour
ma question est toute bete j'aimerais juste savoir pour quoi on ne prend pas en consideration (x-1)

@loicstephan , re-bonjour,

$f (x) = x - 1 + l n (3 - x)$

Pour tout x réel, (x-1) existe, donc il n'y a aucune condition à imposer relativement à (x-1)
Par contre, ln(3-x) existe si et seulement si (x-3) est strictement positif, d'où la condition $x<3x\lt 3$

@mtschoon a dit dans Intersection avec les axes :

@Simaths , tu as dû voir le théorème des valeurs intermédiaires en cours.

Je pense que tu as trouvé:
$Df=]−∞,3[D_f=]-\infty,3[$
f strictement croissante sur $]−∞,2[]-\infty,2[$
f strictement décroissante sur $] 2, 3 [$
maximum pour $x = 2$ : $f (2) = 1$

D'après le TVI,
f est définie, continue et strictement croissante de $]−∞,2[]-\infty,2[$ vers $]−∞,1[]-\infty,1[$
$0∈]−∞,1[0\in ]-\infty,1[$
Il existe donc une valeur unique $α\alpha$ de $]−∞,2[]-\infty,2[$ telle que $f(α)=0\boxed{f(\alpha)=0}$
A la calculette, $α≈−0.15\boxed{\alpha\approx -0.15}$

Tu raisonnement de la même manière sur l'intervalle $] 2, 3 [$ où tu trouveras une valeur $β\beta$ telle que $f(β)=0f(\beta)=0$
(Tu dois trouver $β≈2,85)\beta \approx 2,85)$

La représentation graphique de f coupe l'axe des abscisses aux points de coordonnées $(α,0)(\alpha,0)$ et $(β,0)(\beta,0)$

2 est la valeur qui annulle la derrivee si non coment t$vous optenez l'interval!

Tout à fait @loicstephan ,

La question de @Simaths était seulement sur les intersections avec les axes de coordonnées .
Il (elle) avait déjà étudié la fonction , donc sa question n'était pas sur la dérivée.

Si tu l'as calculé, tu as dû trouver, après transformations :
$f′(x)=x−2x−3f'(x)=\dfrac{x-2}{x-3}$
Tu peux, si ça t'interesse, étudier le signe de f'(x) sur $]−∞,3[]-\infty,3[$ , puis les variations de f.

@mtschoon ok, donc si je comprends très bien on peut seulement trouver ces points seulement à l'aide d'une machine, mais avec les méthodes c'est pas possible ?

@mtschoon bonsoir ! coomet allez vous!
c'est bon j'avais une erreur dans ma derrivee la condition d'esxistence de f'(x) corobore meme avec le Df

@mtschoon a dit dans Intersection avec les axes :

@Simaths , tu as dû voir le théorème des valeurs intermédiaires en cours.

Je pense que tu as trouvé:
$Df=]−∞,3[D_f=]-\infty,3[$
f strictement croissante sur $]−∞,2[]-\infty,2[$
f strictement décroissante sur $] 2, 3 [$
maximum pour $x = 2$ : $f (2) = 1$

D'après le TVI,
f est définie, continue et strictement croissante de $]−∞,2[]-\infty,2[$ vers $]−∞,1[]-\infty,1[$
$0∈]−∞,1[0\in ]-\infty,1[$
Il existe donc une valeur unique $α\alpha$ de $]−∞,2[]-\infty,2[$ telle que $f(α)=0\boxed{f(\alpha)=0}$
A la calculette, $α≈−0.15\boxed{\alpha\approx -0.15}$

Tu raisonnement de la même manière sur l'intervalle $] 2, 3 [$ où tu trouveras une valeur $β\beta$ telle que $f(β)=0f(\beta)=0$
(Tu dois trouver $β≈2,85)\beta \approx 2,85)$

La représentation graphique de f coupe l'axe des abscisses aux points de coordonnées $(α,0)(\alpha,0)$ et $(β,0)(\beta,0)$

f est définie, continue et strictement croissante de ]−∞,2[]-\infty,2[]−∞,2[ vers ]−∞,1[]-\infty,1[]−∞,1[
0∈]−∞,1[0\in ]-\infty,1[0∈]−∞,1[ je comprend bien ces notion ce que je veux savoir c'est d'apres le table de variation la derrivee est pisitive sur l'interval $] - \infty, 2 [$ donc la fonction est croissante sur cet interval la limite en $- \infty$ est egale a $- \infty$ l'image de 2 est 1 donc la fonction croit de ]−∞,1[ ce que je ne comprend pas est l'espression"" croissante de ]−∞,2[]-\infty,2[]−∞,2[ vers ]−∞,1[]-\infty,1[]−∞,1[""
pour quoi avoifr inclue l'interval ]−∞,1[ sachant que la fonction est belle et bien definie continue sur ]−∞,2[ pour l'application du TVI sachant egalement que l'interval ]−∞,1[ est compris dans ]−∞,2[

@Simaths a dit dans Intersection avec les axes :

@mtschoon ok, donc si je comprends très bien on peut seulement trouver ces points seulement à l'aide d'une machine, mais avec les méthodes c'est pas possible ?

De quelles méthodes parles-tu ?
Le calcul en utilisant la calculatrice a été indiqué.

Bonjour,

@loicstephan ,
Dans cet exercice, pour trouver les intervalles utiles pour appliquer le TVI, il faut avoir étudié les variations de f, les limites aux bornes de l'ensemble de définition, et avoir ainsi le tableau de variation complet (avec les limites).
Ainsi, les intervalles utiles sont apparents (intervalle pour x et intervalle associé pour f(x)).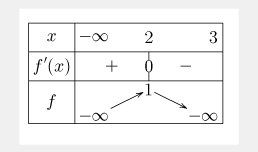

Si besoin, je te mets un lien sur le thoérème des valeurs intermédiairesn ses coromaires et des exemples. http://maths.desfontaines.free.fr/IMG/pdf/Quand_et_comment_utiliser_le_theoreme_des_valeurs.pdf

@Simaths a dit dans Intersection avec les axes :

@mtschoon ok, donc si je comprends très bien on peut seulement trouver ces points seulement à l'aide d'une machine, mais avec les méthodes c'est pas possible ?

@Simaths , il faut que tu fasses la différence entre les valeurs réelles exactes $α\alpha$ et $β\beta$ et leurs valeurs approchées.
Le TVI a prouvé l'existence de ces valeurs réelles exactes, et la "machine" permet d'en trouver les valeurs approchées.

Un exemple qui n'a absolumenrt rien à voir, mais peut-être pour t'aider à comprendre.
En géométrie, le périmètre d'un cercle de rayon R est $2πR2\pi R$

$π\pi$ est un nombre réel (irrationnel)
Il a été nommé par une lettre car il ne pouvait pas s'exprimer parfaitement avec des "chiffres"
$π≈3.14159...\pi\approx 3.14159...$
Si tu préfères, $3.14159<π<3.141603.14159\lt \pi\lt 3.14160$
$3.14159$ , $3.14160$ , etc, ... ne sont que des valeurs approchées de $π\pi$

@Noemi bonsoir,
Je parle de la méthode de sans calculette pour trouver alpha et belta

@loicstephan on ne considère pas x-1 parce que son Df est dans R

@Simaths

Sans calculette, tu peux éventuellement faire une lecture graphique.

Bonsoir,

@Simaths ,
Sans "outil" (une calculette par exemple) tu ne peux pas connaître toutes les valeurs de la fonction logarithme népérien , donc connaître toutes les valeurs de la fonction f.

Je pense que s'il s'agissait d'un devoir surveillé à faire sans calculette, avec les mêmes questions que pour cet énoncé (demandant une représentation graphique précise, des valeurs numériques approchées de $α\alpha$ et $β\beta$ ), il y aurait en annexe au sujet, un tableau numérique où les valeurs utiles seraient indiquées.