Equation de droites, perpendiculaires

Bonjour,est-ce que tu peux m'aider dans cette équation
On a : A(2;3) B(-1;-3) D(4;2) C (1;-4)

déterminer l'équation des droites (AC) et (BD)
J'ai compris cette question
Déduire que les droites (AC) et (BD) sont perpendiculaires
Je n'ai pas compris cette question

@MED-Amine-Sayar Bonjour,

Deux droites sont perpendiculaires si le produit de leur coefficient directeur est égal -1.

Ou applique le produit scalaire;
Deux droites sont orthogonales si leur vecteur directeurs sont orthogonaux, c'est à dire que le produit scalaire de ces deux vecteurs est nul.

@Noemi le coefficient de (AC) est 7 et le coefficient de (BD) est 1 mais le produit de coefficient est égale à 7

@MED-Amine-Sayar

A mon avis, tu as une erreur dans l'énoncé pour les coordonnées des points C ou D.
Vérifie l'énoncé.

@Noemi (AC) :y=ax+b
On détermine a:
a=yc-ya/xc-xa = -4-3/1-2 = 7
(AC) :y=7x+b
On a :A(2;3) appartient (AC) Donc x=2 et y=3
3=7×2+b
b=-11 alors (AC) :y=7x-11

@Noemi (BD) : y=mx+p
On détermine m
m= yd-yb/xd-xb = 2-(-3)/4-(-1) = 1
Donc (BD) y= x+b
B(-1;-3) appartient (BD) donc x = -1 et y=-3
-3=-1+p p= -2
Alors (BD):y=x-2

@MED-Amine-Sayar

Les calculs sont corrects, comme $7×1=77\times1=7$ différents de - 1, les deux droites ne sont pas perpendiculaires.

Fait le même calcul pour (AD) et (BC).

Tu n'as pas vu le produit scalaire en cours ?

@Noemi D'accord Monsieur

@Noemi est égale à -1/2×-1/2=1

@MED-Amine-Sayar

Attention $(−12)×(−12)=14(-\dfrac{1}{2})\times (-\dfrac{1}{2})= \dfrac{1}{4}$
Donc les droites (AD) et (BC) ne sont pas perpendiculaires.

Vérifie l'énoncé.

@Noemi d'accord
Mais on conclus que (AD) //(BC)

Bonjour,

Les droites (AC) et (BD) sont bien perpendiculaires.

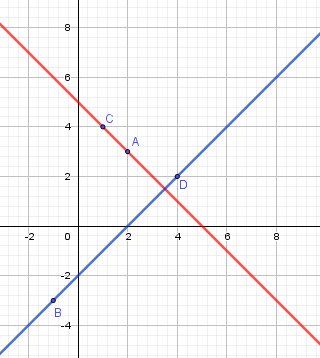
@mtschoon a dit dans Equation de droites, perpendiculaires :

Bonjour,

Avec les notations de l'énoncé, les droites (AC) et (BD) sont bien perpendiculaires.

Bonjour mtschoon et MED Amine Sayar,

L'erreur possible dans l'énoncé est ainsi peut-être repérée. Car l'énoncé indique pour les coordonnées du point C : $(1; - 4)$ et non $(1; 4)$ tel que proposé sur la figure.

Oui @Noemi , c'est bien (1,4) pour C, pour que les droites soient perpendiculaires.

(Je l'ai pris" d'instinct" sur mon schéma...)

@MED-Amine-Sayar ,
Tu devrais revoir tes calculs avec (1,4) pour C.

Si l'on parle de vecteurs :
$AC→\overrightarrow{AC}$ a pour coordonnées (-1,1)
$BD→\overrightarrow{BD}$ a pour coordonnées (5,5)

Si l'on parle des coefficients directeurs des droites
(AC) a pour coefficient directeur a=-1
(BD) a pour coefficient directeur a'=1

$a×a′=−1a\times a'=-1$

@mtschoon C'est C(1;4) oui merci beaucoup

@MED-Amine-Sayar , de rien !

J'espère que maintenant tout est bon pour toi, sinon reposte.

Bon travail !

@mtschoon Oui, merci beaucoup

@Noemi Merci beaucoup